Q.ys In the xy-plane, the length of the shortest path from (0.0) to (12.16) that does not go inside the circle 6) (y-8) 25 is (D) 10 (B) 10 5 (A) 10 Dps' on Circle
A
10√3
B
10√5
C
10√3+5π3
D
10+5π
Video Solution
Text Solution
The correct Answer is:C
Let O≡(0,0)P≡(6,8) and Q≡(12,16).
As shown in the figure, the shortest route consists of tangent OT, minor arc TR and tangent RQ.
Since OP=10,PT=5, and ∠OTP=90∘, it follows that ∠OPT=60∘and OT=5√3.
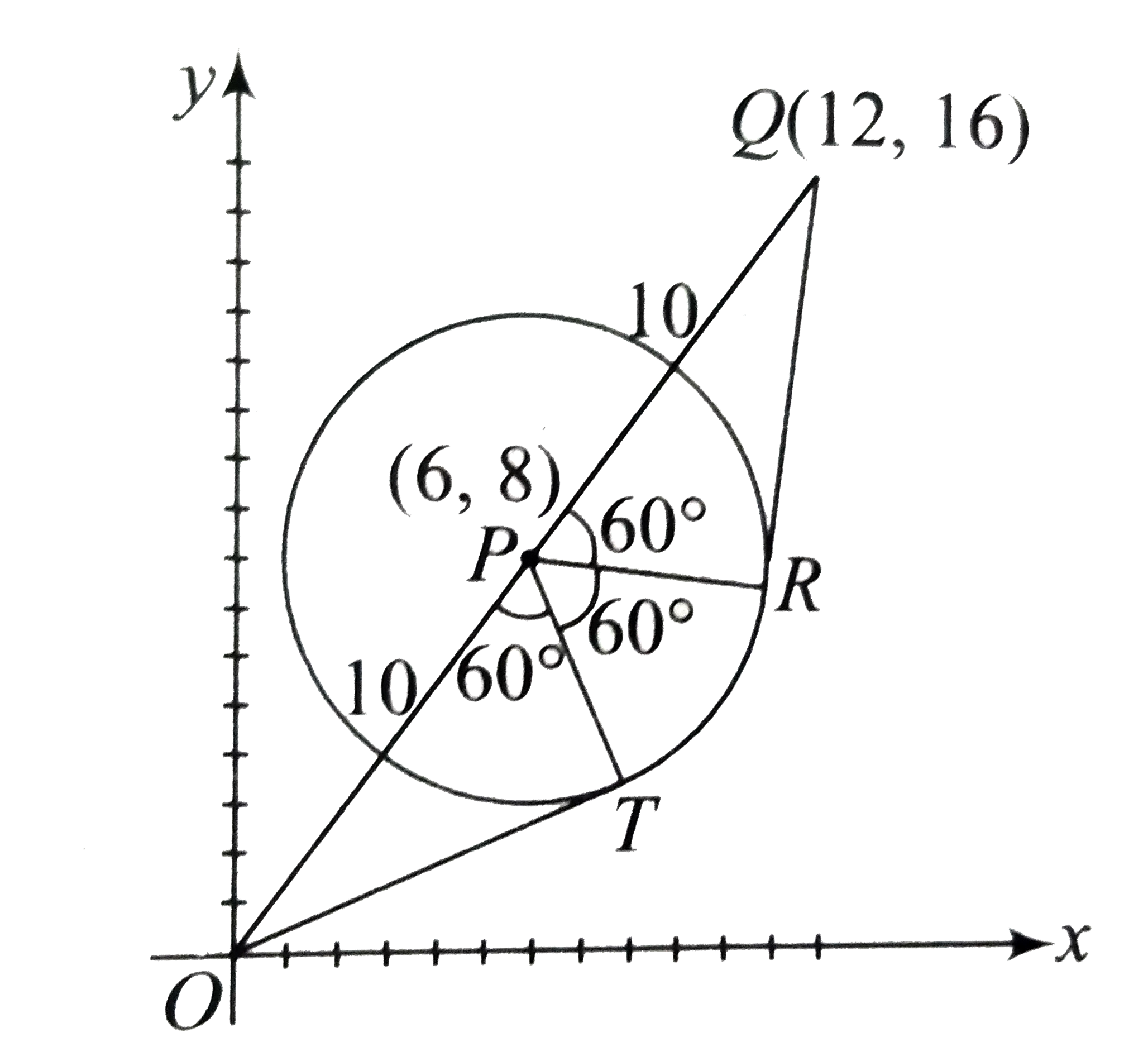
Similarly, PQ=10 and PR=5
∴∠QPR=60∘ and QR=5√3
Also points O,P and Q are collinear as mOP=mPQ
Thus, ∠RPT=60∘ and arc TR is of length 5π3.
Hence, the length of the shortest route is 2(5√3)+5π3.
|
Topper's Solved these Questions
- CIRCLESBOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Question Bank
32 Videos
- CIRCLESBOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Comprehension Type
8 Videos
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - JEE Advanced (Single Correct Answer Type)
14 Videos
- COMPLEX NUMBERSBOOK - CENGAGECHAPTER - COMPLEX NUMBERSEXERCISE - Question Bank
30 Videos
Similar Questions
Knowledge Check
Find the centre of the circle x2+y2−8x+10y−12=0.
A(4,−5)B(−4,−5)C(4,5)DNone of theseThe centre of a circle passing through the points (0, 0), (1, 0) and touching the circle x2+y2=9, is
A(32,12)B(12,32)C(12,12)D(12,−21/2)Find the centre of the circle x2+y2+8x+10y−8=0.
A(4,−5)B(−4,−5)C(4,5)DNone of these
The shortest distance from the point (0,5) to the circumference of the circle x2+y2−10x+14y−151=0 is: (A) 13 (B) 9 (C) 2 (D) 5
View SolutionIn the xy plane, the segment with end points (3,8) and (-5,2) is the diameter of the circle. The point (k,10) lies on the circle for
View SolutionFind the shortest distance from the point M(−7,2) to the circle x2+y2−10x−14y−151=0.
View SolutionThe length of the tangent from a point on the circle x2+y2+4x–6y−12=0 to the circle x2+y2+4x–6y+4=0 is
View SolutionThe length of the shortest chord of the circles x2+y2+2gx+2fy+c=0 which passes through the point (a, b) inside the circle is
View Solution
