Replace A,B and C by suitable numerals. 4CB6+369A 8173
The correct Answer is:A=7, B=7, C=4
To solve the problem of replacing A, B, and C with suitable numerals in the equation (4CB6)+(369A)=8173, we will follow these steps:
Step 1: Set Up the Equation
We start with the equation:
(4CB6)+(369A)=8173
Step 2: Identify the Last Digit
We look at the last digits of both numbers:
- The last digit of 4CB6 is 6.
- The last digit of 369A is A.
Adding these gives:
6+A≡3mod10
This means that 6+A must end in 3. The possible values for A can be calculated as follows:
- If A=7, then 6+7=13 (last digit is 3).
Thus, we have:
A=7
Step 3: Substitute A and Analyze the Next Column
Now we substitute A into the equation:
(4CB6)+(3697)=8173
Step 4: Identify the Second Last Digit
Next, we look at the second last digits:
- The second last digit of 4CB6 is B.
- The second last digit of 3697 is 9.
Adding these gives:
B+9+1≡7mod10
(The 1 is the carry from the previous addition of 6+7).
This simplifies to:
B+10≡7mod10
Thus, B must be:
B=7−10=−3(not possible)
So we try B+9+0≡7mod10:
B+9≡7mod10
This means:
B≡7−9≡−2≡8mod10
Thus, we have:
B=8
Step 5: Substitute B and Analyze the Third Column
Now we substitute B into the equation:
(48C6)+(3697)=8173
Step 6: Identify the Third Last Digit
Next, we look at the third last digits:
- The third last digit of 48C6 is C.
- The third last digit of 3697 is 6.
Adding these gives:
C+6+1≡1mod10
(The 1 is the carry from the previous addition of B+9).
This simplifies to:
C+7≡1mod10
Thus:
C≡1−7≡−6≡4mod10
Thus, we have:
C=4
Final Values
Now we have found:
- A=7
- B=8
- C=4
Conclusion
The values of A, B, and C are:
A=7,B=8,C=4
We start with the equation:
(4CB6)+(369A)=8173
We look at the last digits of both numbers:
- The last digit of 4CB6 is 6.
- The last digit of 369A is A.
6+A≡3mod10
This means that 6+A must end in 3. The possible values for A can be calculated as follows:
- If A=7, then 6+7=13 (last digit is 3).
A=7
Now we substitute A into the equation:
(4CB6)+(3697)=8173
Next, we look at the second last digits:
- The second last digit of 4CB6 is B.
- The second last digit of 3697 is 9.
B+9+1≡7mod10
(The 1 is the carry from the previous addition of 6+7).
B+10≡7mod10
Thus, B must be:
B=7−10=−3(not possible)
So we try B+9+0≡7mod10:
B+9≡7mod10
This means:
B≡7−9≡−2≡8mod10
Thus, we have:
B=8
Now we substitute B into the equation:
(48C6)+(3697)=8173
Next, we look at the third last digits:
- The third last digit of 48C6 is C.
- The third last digit of 3697 is 6.
C+6+1≡1mod10
(The 1 is the carry from the previous addition of B+9).
C+7≡1mod10
Thus:
C≡1−7≡−6≡4mod10
Thus, we have:
C=4
Now we have found:
- A=7
- B=8
- C=4
The values of A, B, and C are:
A=7,B=8,C=4
Topper's Solved these Questions
- BOOK - RS AGGARWALCHAPTER - PLAYING WITH NUMBERSEXERCISE - Exercise 5D9videos
PLAYING WITH NUMBERS
- BOOK - RS AGGARWALCHAPTER - PLAYING WITH NUMBERSEXERCISE - Test Paper-511videos
PLAYING WITH NUMBERS
- BOOK - RS AGGARWALCHAPTER - PLAYING WITH NUMBERSEXERCISE - Exercise 5B15videos
PLAYING WITH NUMBERS
- BOOK - RS AGGARWALCHAPTER - PIE CHARTS EXERCISE - Exercise 24B4videos
PIE CHARTS
- BOOK - RS AGGARWALCHAPTER - POLYGONSEXERCISE - EXERCISE 14B14videos
POLYGONS
Similar Questions
Knowledge Check
- Question 1 - Select One
Replace A,B,C by suitable numberals:
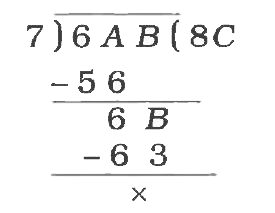 AA=1,B=3,C=9BA=2,B=3,C=9CA=1,B=6,C=9DA=1,B=6,C=8
AA=1,B=3,C=9BA=2,B=3,C=9CA=1,B=6,C=9DA=1,B=6,C=8
Replace A,B and C by suitable numerals. 6A−AB 37
View SolutionReplace A,B and C by suitable numerals. 5A+87 CB3
View SolutionReplace A,B and C by suitable numerals. AB×BA (B+1)CB
View SolutionReplace A,B and C by suitable numerals. A+A A BA
View SolutionReplace A,B,C by suitable numberals:
57A−CB8 293View SolutionReplace A,B,C,D by suitable numerals in the following
6AB5+D58C 9351View SolutionFind the values of A,B and C in the following
35A−CB8 183View Solution

