S and T are points on sides PR and QR of $Δ P Q R$ such that $∠ P = ∠ R T S$ . Show that $Δ R P Q ~ Δ R T S$ .

Video Solution

Text Solution

Verified by Experts

In $∠ R P Q and ∠ R T S$
$∠ R P Q = ∠ R T S$ given)
$∠ P R Q = ∠ T R S$ (same angles)
A-A similarity criteria
$∠ R P Q ~ ∠ R T S$

|

Updated on:21/07/2023

Class 10 MATHS TRIANGLES

Similar Questions

S and T are points on sides PR and QR of $Δ P Q R$ such that $∠ P = ∠ R T S$ . Show that $Δ R P Q ~ Δ R T S$ .
View Solution
S and T are points on sides PR and QR of $Δ P Q R$ such that $∠ P = ∠ R T S$ Show that $Δ R P Q ~ Δ R T S$
View Solution
In the given figure, S and T are points on sides PR and QR of $Δ P Q R$ such that $∠ P = ∠ R T S$ . Show that $Δ R P Q ~ Δ R T S$ .

View Solution
In Fig. 4.238, $S$ and $T$ are points on the sides $P Q$ and $P R$ respectively of $P Q R$ such that $P T = 2 c m$ , $T R = 4 c m$ and $S T$ is parallel to $Q R$ . Find the ratio of the areas of $P S T$ and $P Q R$ . (FIGURE)
View Solution
In figure $\frac{Q R}{Q S} = \frac{Q T}{P R}$ and $∠ 1 = ∠ 2$ . Show that $Δ P Q S ~ Δ T Q R$ .

View Solution
In figure Cm and RN are respectively the medians of $Δ A B C$ and $Δ P Q R$ . If $Δ A B C ~ Δ P Q R$ , prove that:
(i) $Δ A M C ~ Δ P N R$
(ii) $\frac{C M}{R N} = \frac{A B}{P Q}$
(ii) $Δ C M B ~ Δ R N Q$

View Solution
In Fig. 6.15, $∠ P Q R = ∠ P R Q$ , then prove that $∠ P Q S = ∠ P R T$ .

View Solution
In Fig. 6.39, sides QP and RQ of $Δ P Q R$ are produced to point S and T respectively. If $∠ S P R = 135^{\circ}$ and $∠ P Q T = 110^{\circ}$ , find $∠ P R Q .$

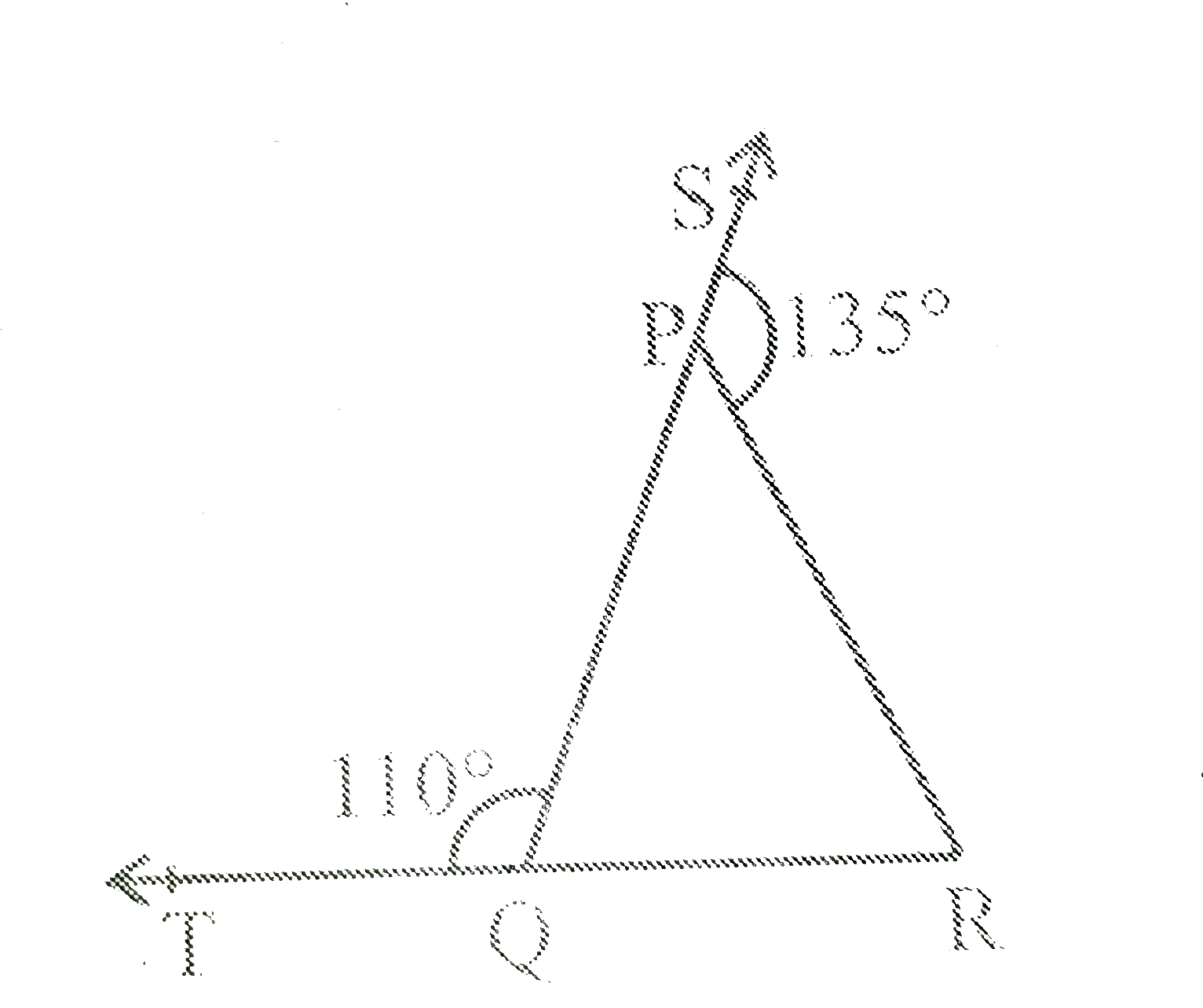View Solution
In Figure, $P Q R S$ is a quadrilateral. $P Q$ is its longest side and $R S$ is its shortest side. Prove that $∠ R > ∠ P a n d ∠ S > ∠ Q$ Given : $P Q R S$ is a quadrilateral. $P Q$ is its longest side and $R S$ is its shortest side. To Prove : (i) $∠ R > ∠ P$ (ii) $∠ S > ∠ Q$ Construction : Joint $P R a n d Q S$

View Solution
In figure PS is the bisector of $∠ Q P R$ of $Δ P Q R$ . Prove that $\frac{Q S}{S R} = \frac{P Q}{P R}$ .

View Solution

Recommended Questions

Home
Ask Doubt
Profile