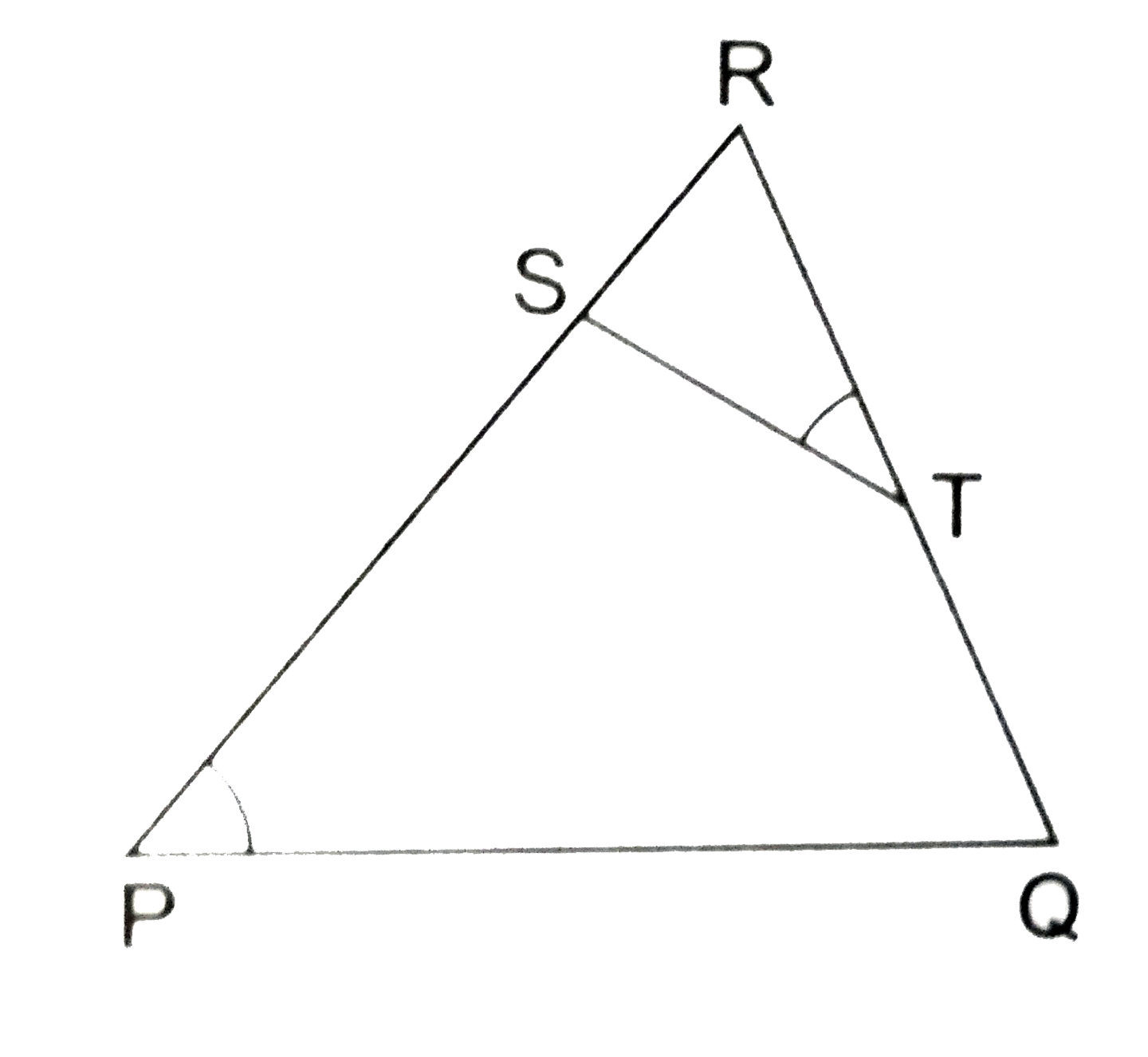
S and T are points on sides PR and QR of ΔPQRsuch that ∠P=∠RTS. Show that ΔRPQΔRTS.
Step by step video solution for S and T are points on sides PR and QR of DeltaP Q Rsuch that /_P=/_R T S. Show that DeltaR P Q DeltaR T S. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- TRIANGLESBOOK - OSWAL PUBLICATIONCHAPTER - TRIANGLESEXERCISE - NCERT CORNER ( TEXTBOOK QUESTIONS) ( EXERCISE - 6.4 )
9 Videos
- TRIANGLESBOOK - OSWAL PUBLICATIONCHAPTER - TRIANGLESEXERCISE - NCERT CORNER ( TEXTBOOK QUESTIONS) ( EXERCISE - 6.5 )
23 Videos
- TRIANGLESBOOK - OSWAL PUBLICATIONCHAPTER - TRIANGLESEXERCISE - NCERT CORNER ( TEXTBOOK QUESTIONS) ( EXERCISE - 6.2 )
12 Videos
- SURFACE AREAS AND VOLUMES BOOK - OSWAL PUBLICATIONCHAPTER - SURFACE AREAS AND VOLUMES EXERCISE - BOARD CORNER (LONG ANSWER TYPE QUESTIONS)
9 Videos
Similar Questions
S and T are points on sides PR and QR of ΔPQRsuch that ∠P=∠RTS. Show that ΔRPQ~ΔRTS.
View SolutionS and T are points on sides PR and QR of ΔPQR such that ∠P=∠RTS Show that ΔRPQ~ΔRTS
View SolutionIn the given figure, S and T are points on sides PR and QR of ΔPQR such that ∠P=∠RTS. Show that ΔRPQ~ΔRTS.
View SolutionIn Fig. 4.238, S and T are points on the sides PQ and PR respectively of PQR such that PT=2cm , TR=4cm and ST is parallel to QR . Find the ratio of the areas of PST and PQR . (FIGURE)
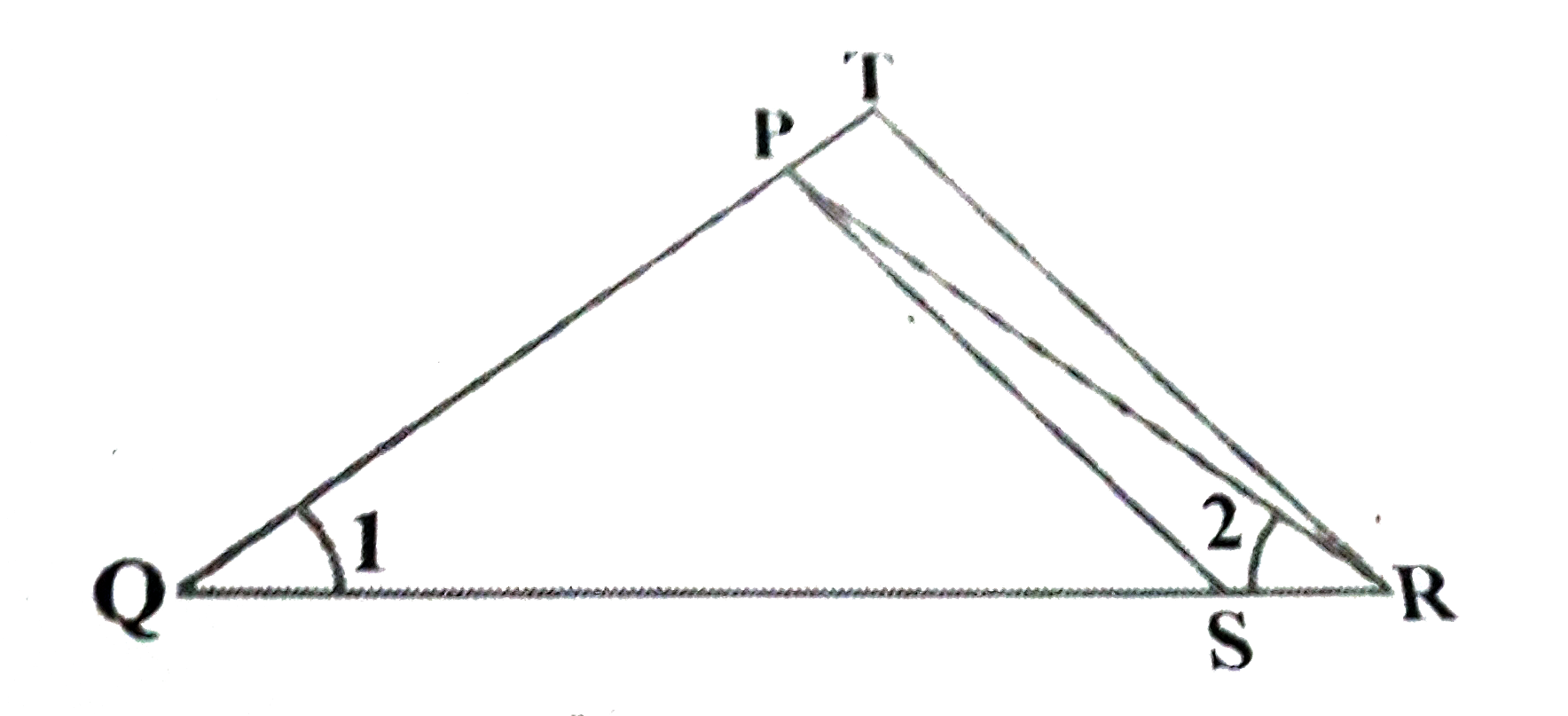
View SolutionIn figure QRQS=QTPRand ∠1=∠2. Show that ΔPQS~ΔTQR.
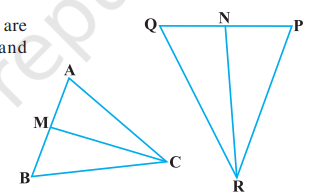
View SolutionIn figure Cm and RN are respectively the medians of ΔABCand ΔPQR. If ΔABC~ΔPQR, prove that:
(i) ΔAMC~ΔPNR
(ii) CMRN=ABPQ
(ii) ΔCMB~ΔRNQ
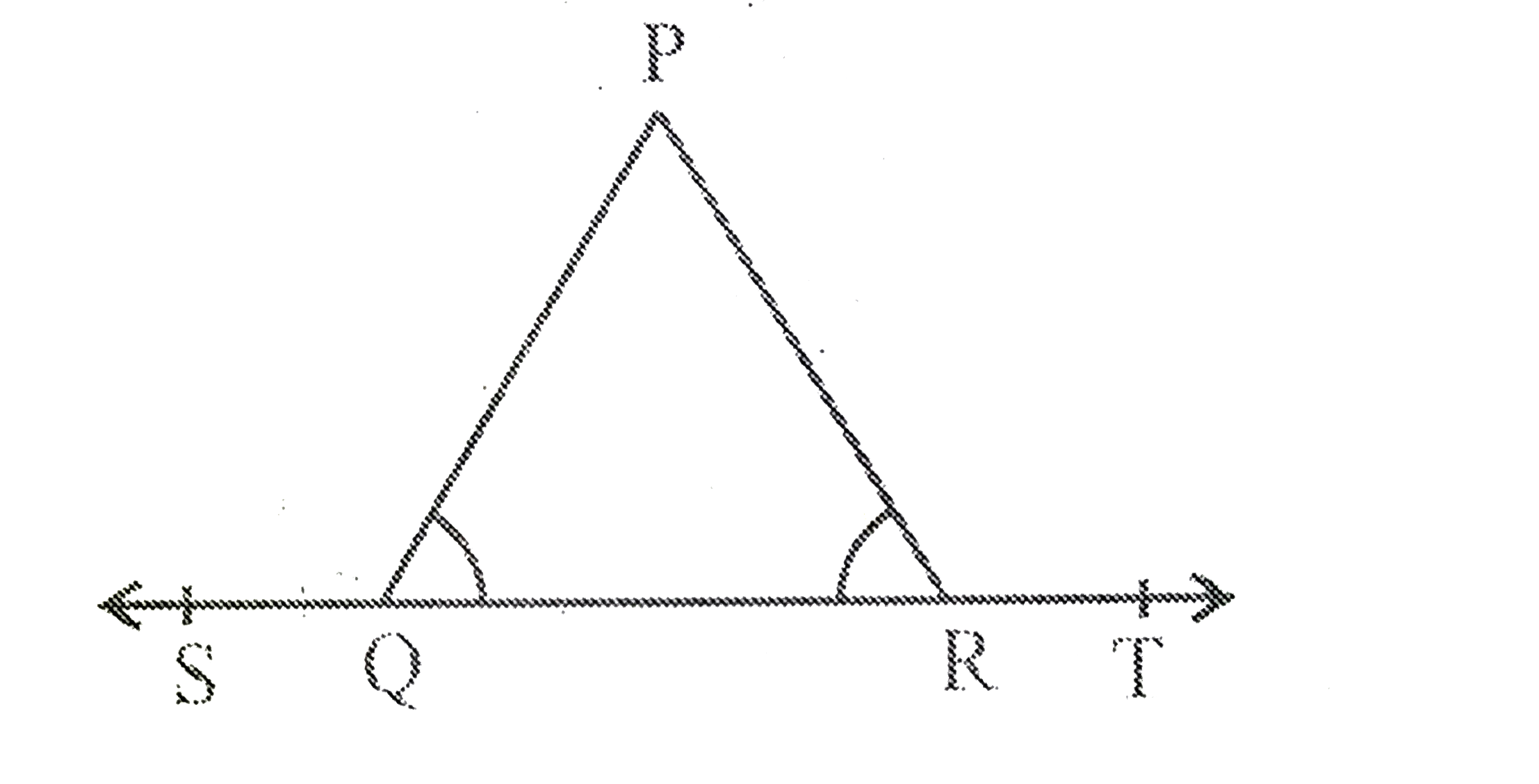
View SolutionIn Fig. 6.15, ∠PQR=∠PRQ, then prove that ∠PQS=∠PRT.
View SolutionIn Figure, PQRS is a quadrilateral. PQ is its longest side and RS is its shortest side. Prove that ∠R> ∠P and ∠S> ∠Q Given : PQRS is a quadrilateral. PQ is its longest side and RS is its shortest side. To Prove : (i) ∠R> ∠P (ii) ∠S> ∠Q Construction : Joint PR and QS
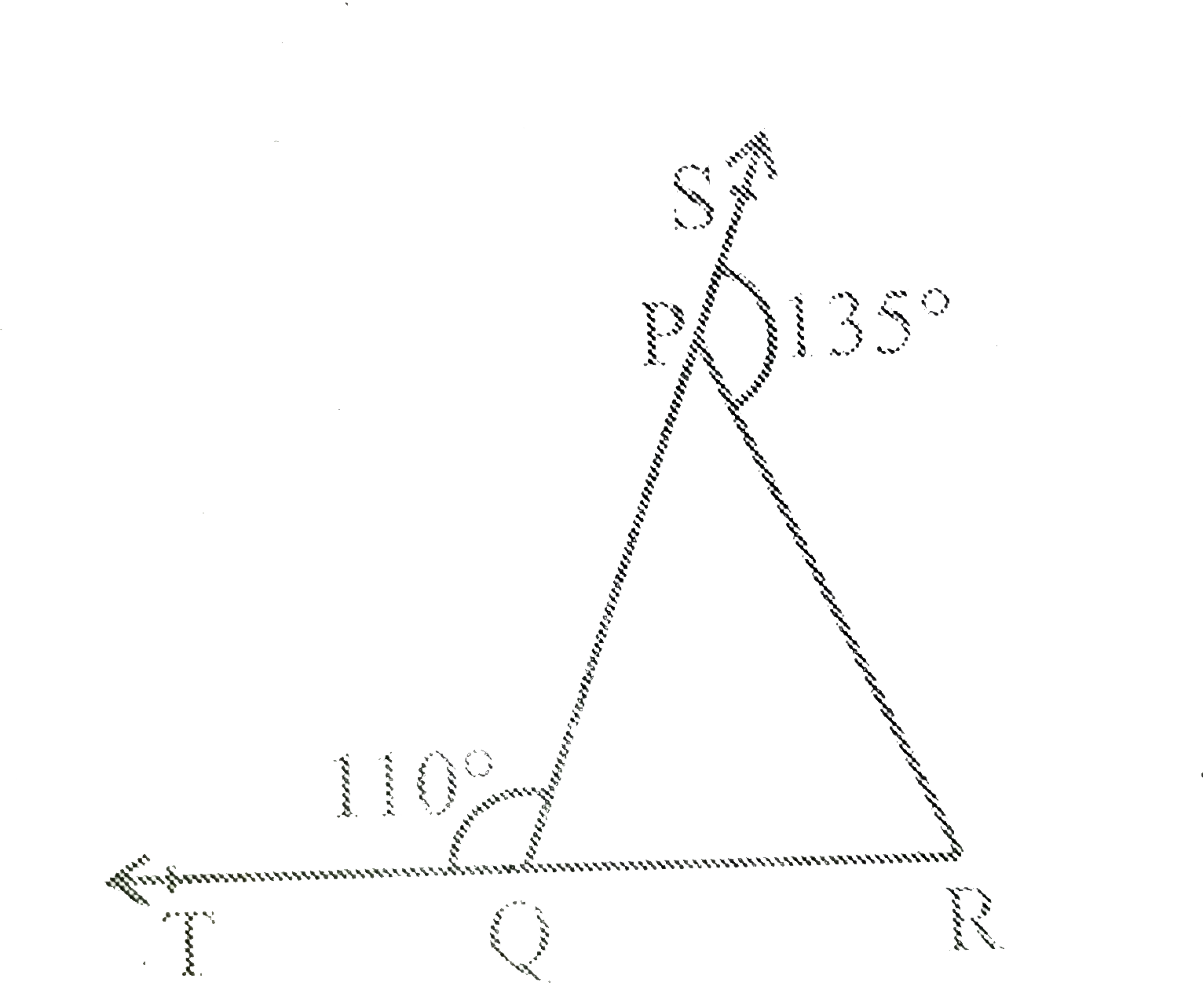
View SolutionIn Fig. 6.39, sides QP and RQ of ΔPQR are produced to point S and T respectively. If ∠SPR=135∘ and ∠PQT=110∘, find ∠PRQ.
View SolutionIn figure PS is the bisector of ∠QPRof ΔPQR. Prove that QSSR=PQPR.
View Solution
