Seg AB is a diameter of a circle with centre P. Seg AC is a chord. A secant through P and parallel to seg AC intersects the tangent drawn at C in D. Prove that line DB is a tangent to the circle.
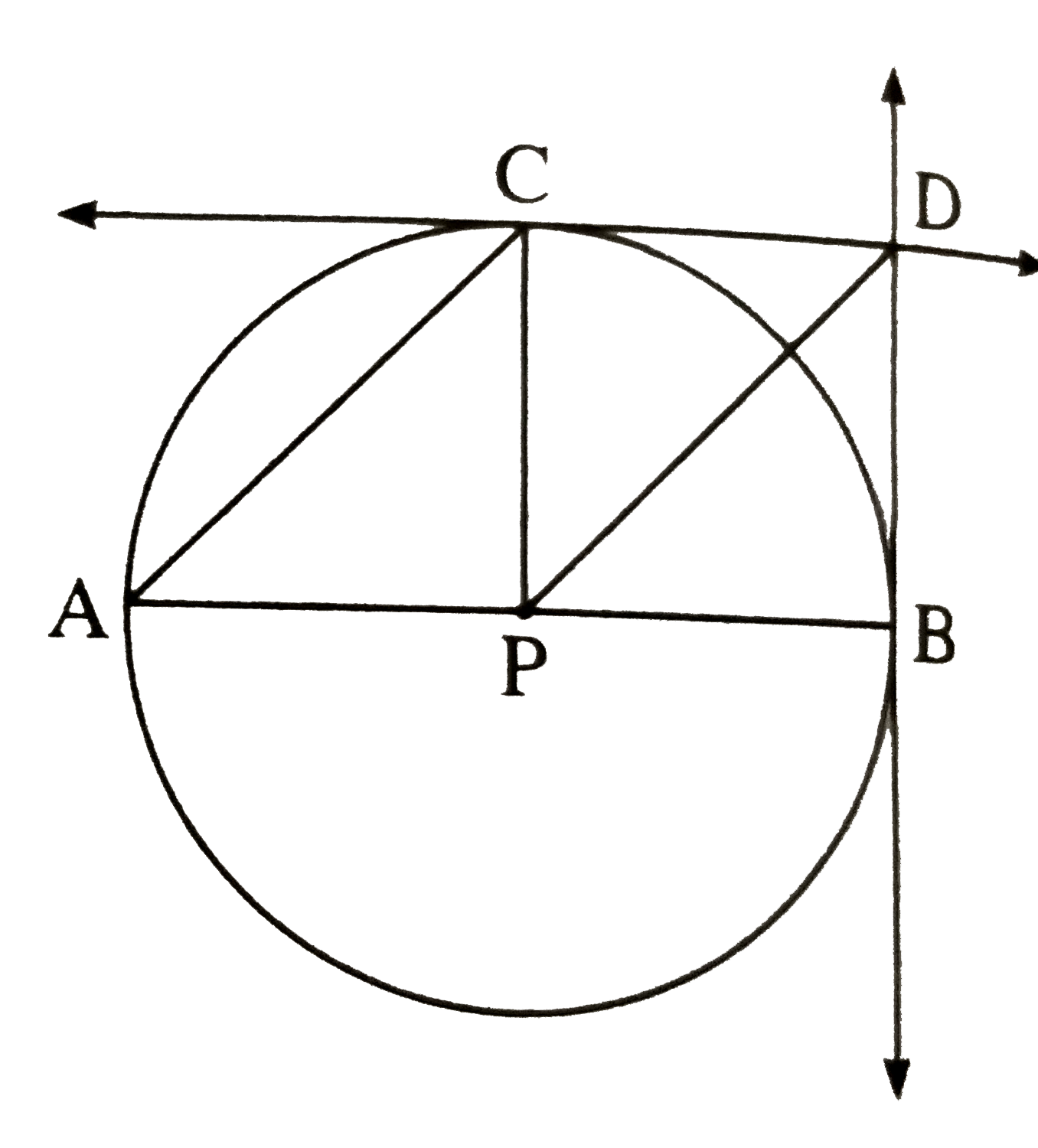
The correct Answer is: by converse of tangent theorem, line BD is tangent to the circle.
Step by step video & image solution for Seg AB is a diameter of a circle with centre P. Seg AC is a chord. A secant through P and parallel to seg AC intersects the tangent drawn at C in D. Prove that line DB is a tangent to the circle. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Topper's Solved these Questions
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CIRCLEEXERCISE - PROBLEM SET 350videos
CIRCLE
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - CHALLENGING QUESTIONSEXERCISE - SECTION 3 (MODEL QUESTION PAPER FOR PRACTICE ) Solve any one of the following subquestions :1videos
CHALLENGING QUESTIONS
- BOOK - NAVNEET PUBLICATION - MAHARASHTRA BOARDCHAPTER - COORDINATE GEOMETRY EXERCISE - Assignment 6.513videos
COORDINATE GEOMETRY
Similar Questions
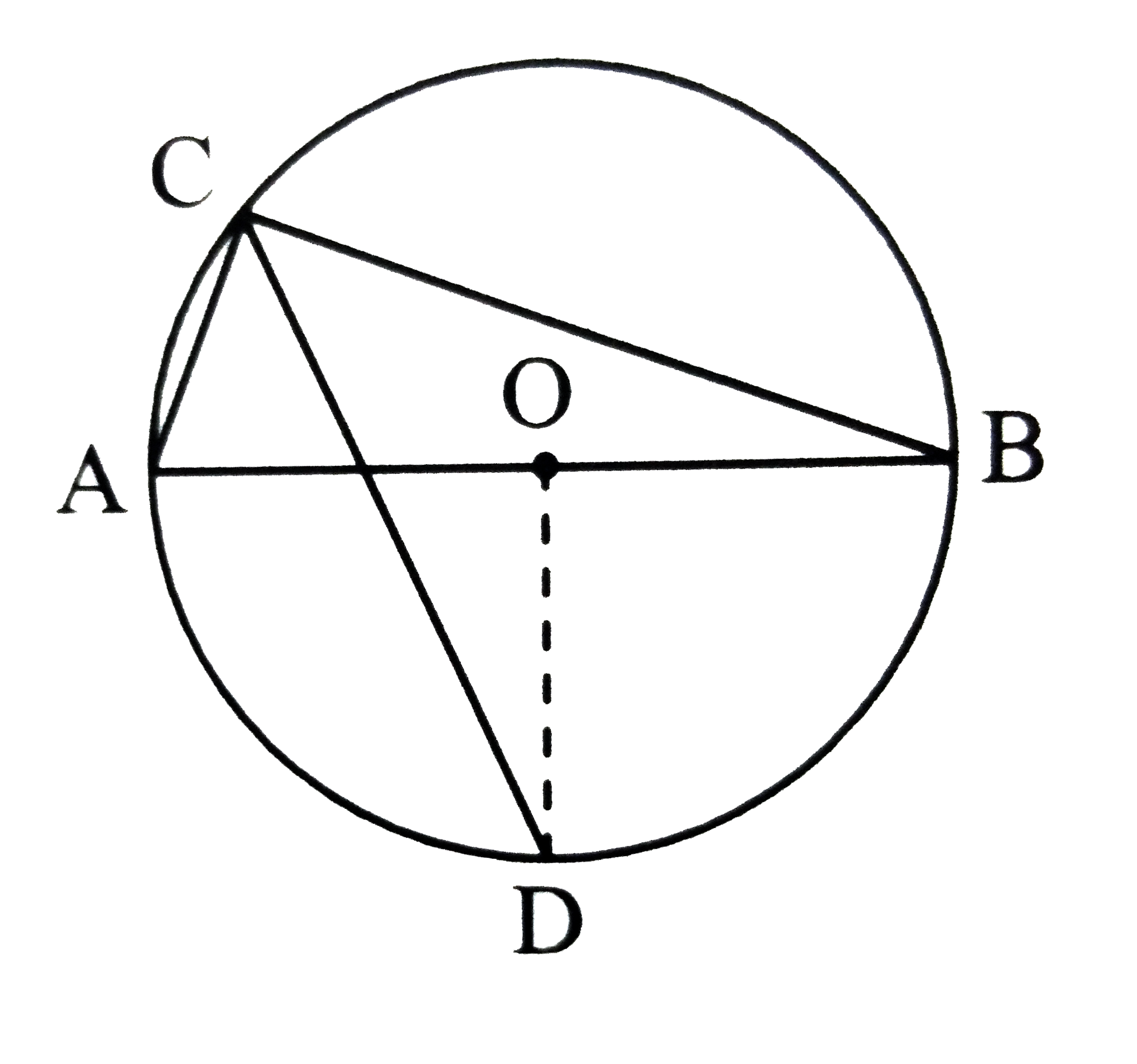
In the adjoining figure, seg AB is a diameter of a circle with centre O. the bisector of ∠ACB intersects the circle at point D. Prove that ,seg AD≅segBD. Complete the following proof by filling the blanks.
 View Solution
View SolutionIn figure, seg AB is a diameter of a circle with centre O. The bisector of ∠ACB intersects the circle at point D. Prove that seg AD ≅ seg BD. Complete the following proof by filling in the blanks
 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
The tangents are drawn at the extremities of diameter AB of a circle with centre P. If a tangent to the circle at the point C Intersects the other two tangents at Q and R, then the measure of the ∠QPR is
A45∘B60∘C90∘D180∘
Two circles whose centres are O and O' intersect at P. Through P, a line l parallel to OO' intersecting the circles at C and D is drawn. Prove that CD=2 OO'
View SolutionAB is a diameter of a circle and AC is its chord such that ∠BAC=30∘. If the tangent at C intersects AB extended at D, then BC=BD.
View SolutionProve that the tangents drawn at the ends of the diameter of a circle are parallel.
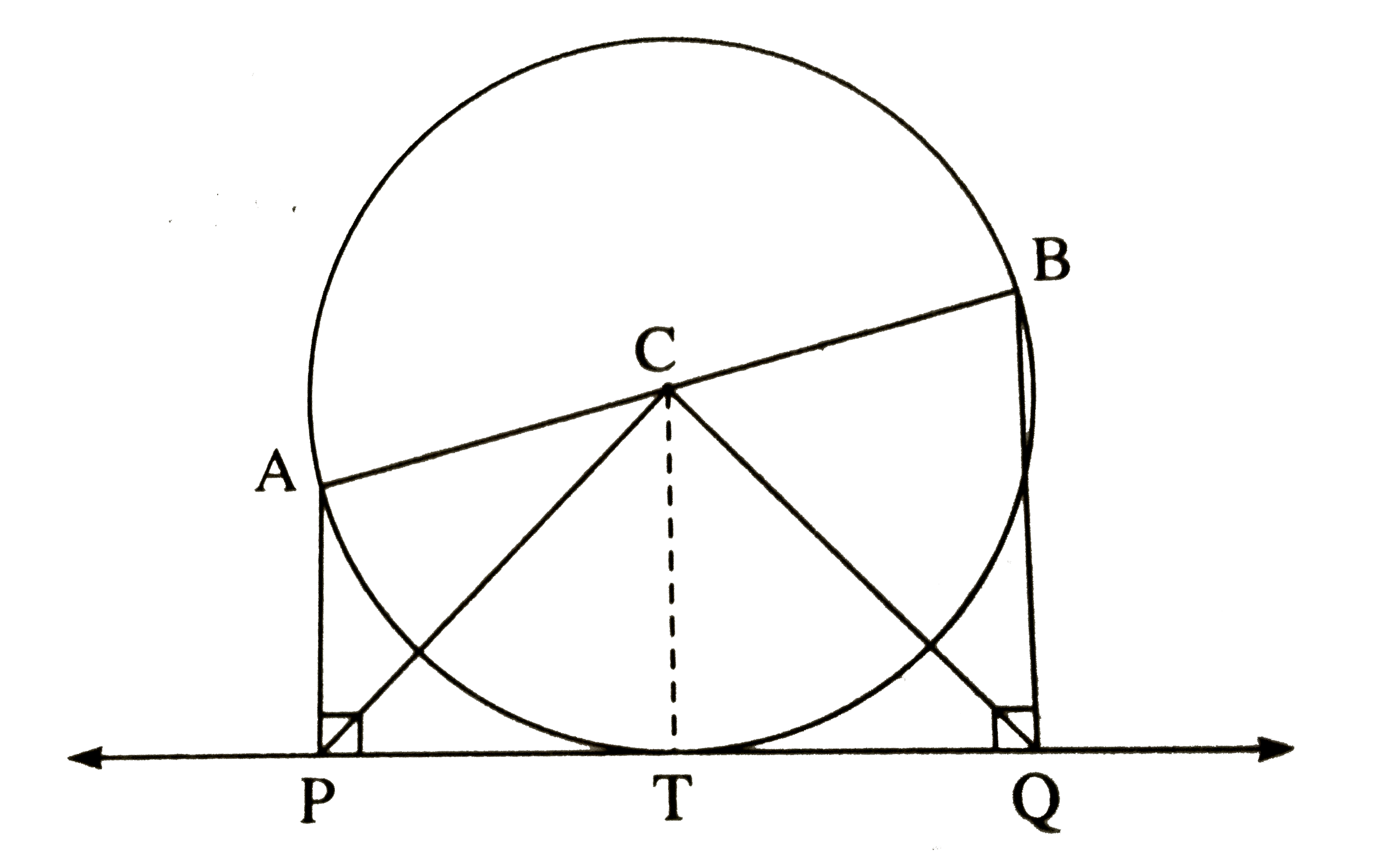
View SolutionIn the figure, seg AB is a diameter of a circle with centre C. Line PQ is a tangent, which touches the circle at point T. seg AP ⊥ line PQ and seg BQ ⊥ line PQ. Prove that, seg CP ≅ seg CQ.
 View Solution
View SolutionIn the figure, seg AB is a diameter of a circle with centre C. Line PQ is a tangent , which touches the circle at point T. seg AP⊥ line PQ and seg BQ⊥ line PQ.
Prove that, seg CP≅ seg CQ.
 View Solution
View Solution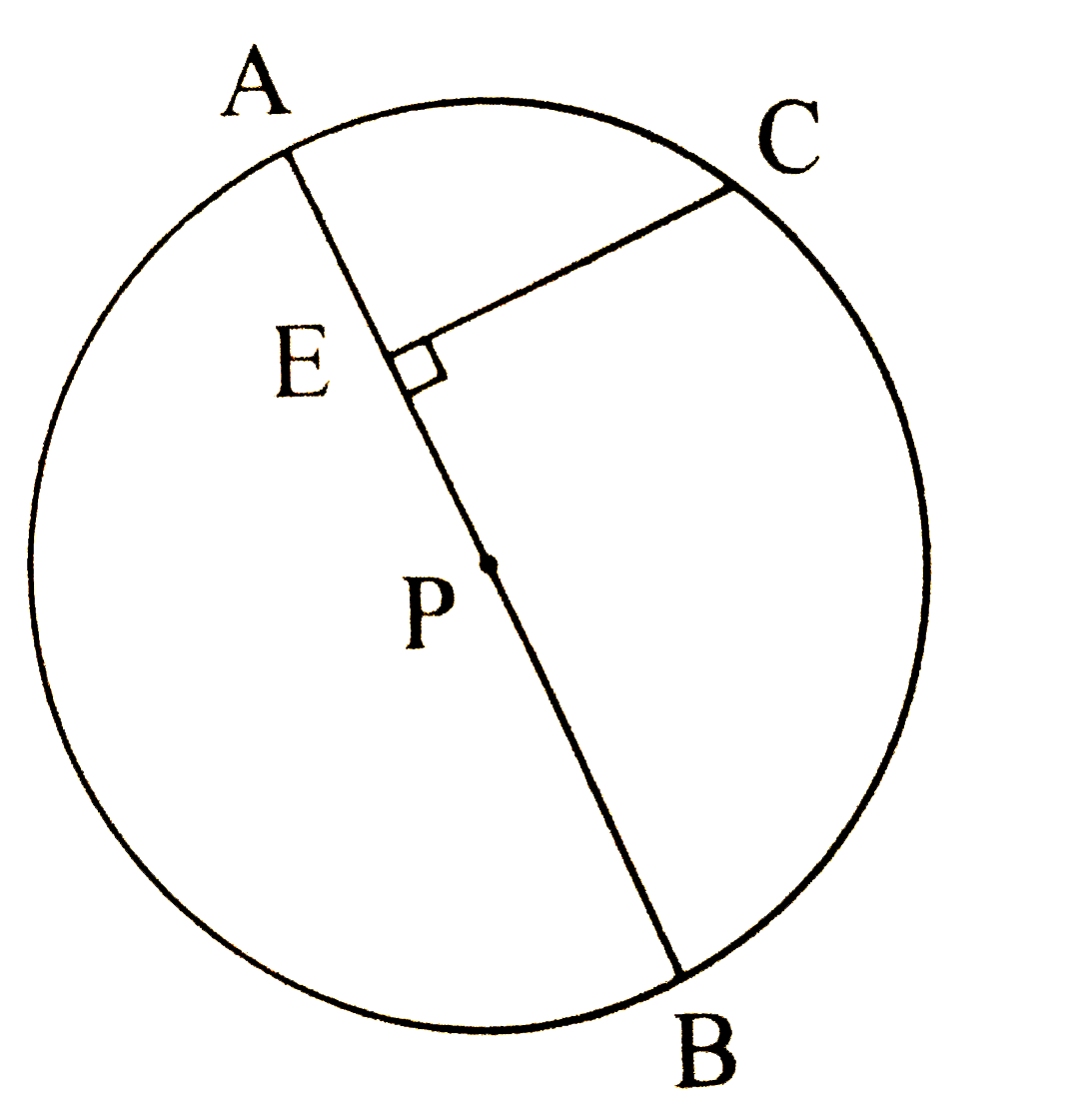
In the above figure, seg AB is a diameter of a circle with centre P.C is any point on the circle. Seg CE ⊥ seg AB. Prove that CE is the geometric mean of AE and EB. Write the proof with the help of folloing steps:
(a) Draw ray CE. It intersects the circle at D.
(b) Show that CE = ED.
Write the result using theorem of intersection of chords insides a circle.
(d) Using CE = ED, complete the proof.View SolutionPoint O is the centre of a circle . Line a and line b are parallel tangents to the circle at P and Q. Prove that segment PQ is a diameter of the circle.
 View Solution
View Solution

