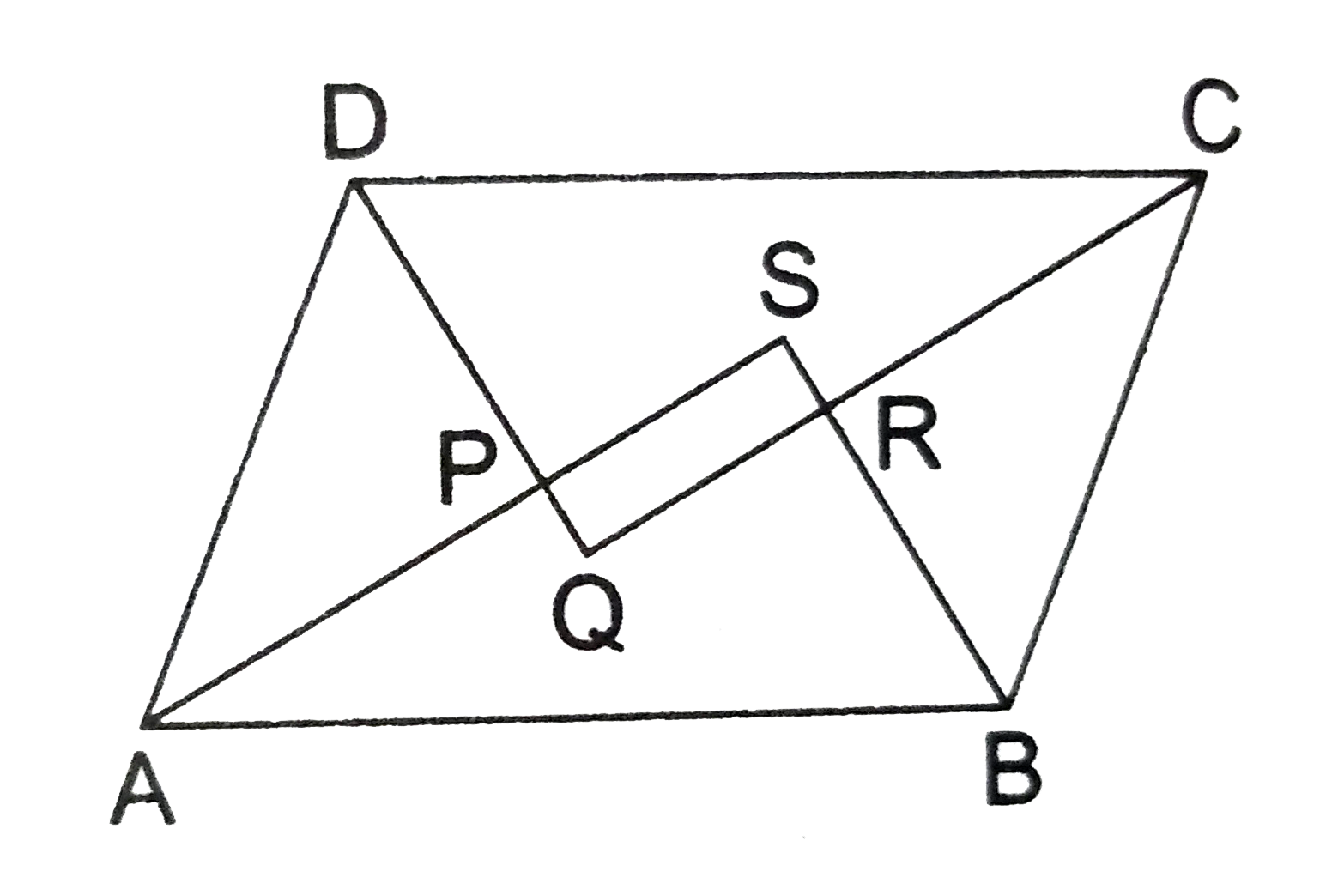
Show that the bisectors of the angles of a parallelogram enclose a rectangle.

Video Solution

Text Solution

Verified by Experts

Since DC||AB and DA cuts them, we have
$∠ A + ∠ D = 180^{\circ} (co-interior ∠)$
$\Rightarrow \frac{1}{2} ∠ A + \frac{1}{2} ∠ D = 90^{\circ}$
$\Rightarrow ∠ P A D + ∠ P D A = 90^{\circ}$
$\Rightarrow ∠ A P D = 90^{\circ} [∵ sum of the ∠ of a △ is 180^{\circ}]$
$\Rightarrow ∠ S P Q = 90^{\circ} (vert. opp. ∠) .$
Now, AD||BC and DC cuts them.
$∴ ∠ D + ∠ C = 180^{\circ} (co-interior ∠)$
$\Rightarrow \frac{1}{2} ∠ D + \frac{1}{2} ∠ C = 90^{\circ}$
$\Rightarrow ∠ Q D C + ∠ Q C D = 90^{\circ}$
$\Rightarrow ∠ D Q C = 90^{\circ} [∵ sum of the ∠ of a △ is 180^{\circ}]$
$\Rightarrow ∠ P Q R = 90^{\circ} .$
Similarly, $∠ Q R S = 90^{\circ} and ∠ R S P = 90^{\circ}$ .
Thus, PQRS is quadrilateral each of whose angles is $90^{\circ} .$
Hence, PQRS is a rectangle.

Updated on:21/07/2023

The bisector of the angles of a parallelogram enclose a
Arectangle
Brhombus
Csquare
Dtrapezium
Consider the following statements
1. The bisectors of all the four angles of a parallelogram enclose a rectangle.
2. The figure formed by joining the midpoints of the adjacent sides of a rectangle is a rhombus.
3. The figure formed by joining the midpoints of the adjacent sides of a rhombus is a square.
Which of these statements are correct ?
A1 and 2
B2 and 3
C3 and 1
D1, 2 and 3
Shape made by the bisectors of angles of a parallelogram is
ARectangle
BSquare
CCircle
DStraight line