Show that the semi vertical angle of a right circular cone of given total surface area and max volume is ${sin}^{- 1} (\frac{1}{3})$

Video Solution

Text Solution

Verified by Experts

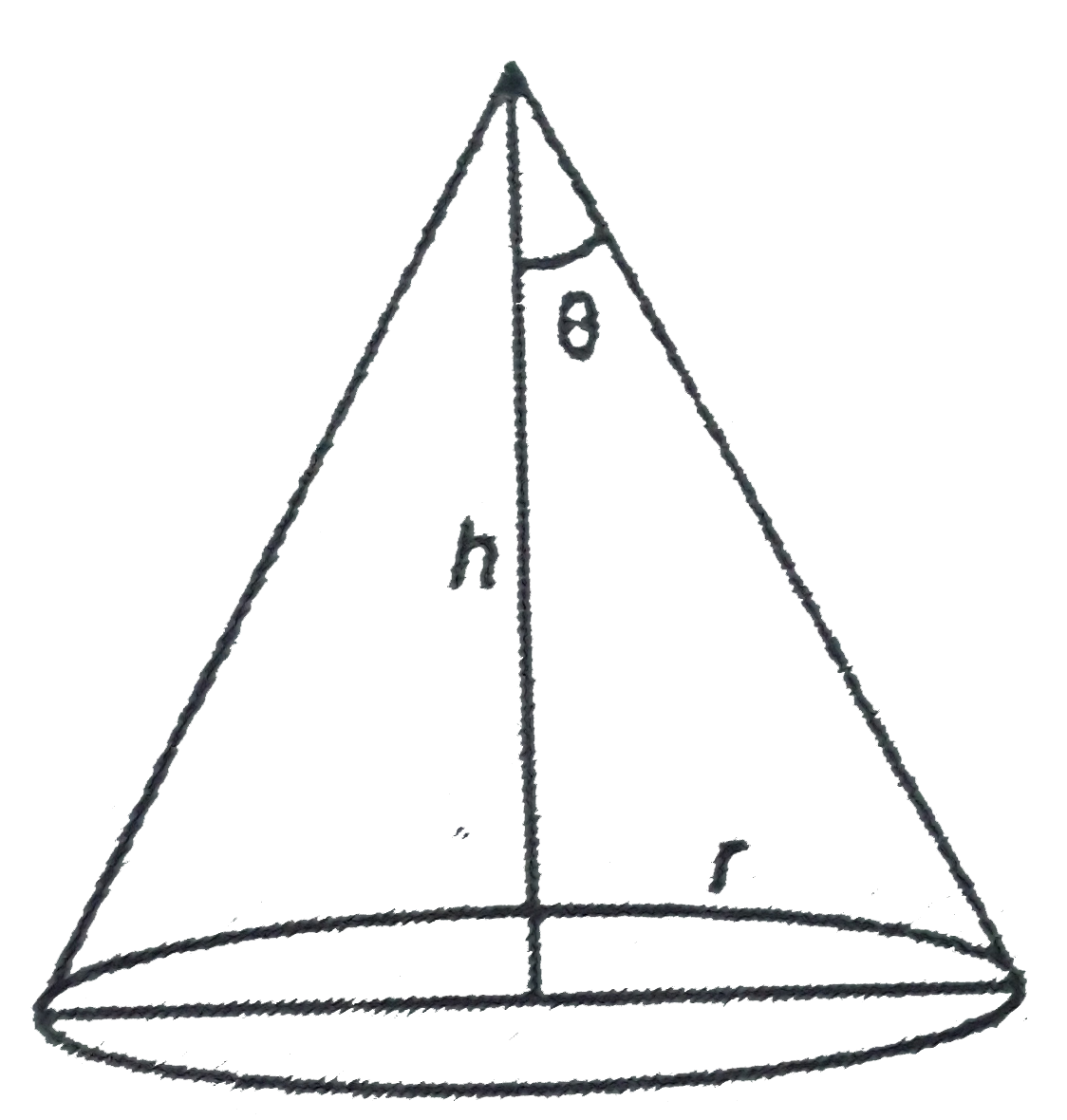
Let the radius of base be 'r', height be 'h' and slant height be 'l' of the cone.
Its total surface area
$S = π r^{2} + π r l$
$\Rightarrow l = \frac{S - π r^{2}}{π r}$
Volume of cone $V = \frac{1}{3} π r^{2} h$
$\Rightarrow V^{2} = \frac{1}{9} π^{2} r^{4} h^{2}$
$V^{2} = \frac{1}{9} π^{2} r^{4} (l^{2} - r^{2})$
$= \frac{1}{9} π^{2} r^{4} [{(\frac{S - π r^{2}}{π r})}^{2} - r^{2}]$
$= \frac{1}{9} π^{2} r^{4} ⎡ ⎣ \frac{{(S - π r^{2})}^{2} - π^{2} r^{4}}{π^{2} r^{2}} ⎤ ⎦$
$\frac{1}{9} r^{2} [S^{2} - 2 π S r^{2}]$
$Z = V^{2} = \frac{S}{9} [S r^{2} - 2 π r^{4}]$
$\frac{d Z}{d r} = \frac{S}{9} [2 S r - 8 π r^{3}]$
Now $\frac{d^{2} Z}{d r^{2} = \frac{S}{9} (2 S - 24 π r^{2})}$
For maxima/minima $\frac{d Z}{d r} = 0$
$\Rightarrow 2 S r = 8 π r^{3}$
$\Rightarrow 2 (π r^{2} + π r l) = 8 π r^{2}$
$\Rightarrow π r l = 3 π r^{2}$
$\Rightarrow l = 3 r \Rightarrow \frac{r}{l} = \frac{1}{3}$
$\Rightarrow sin α = \frac{1}{3} where α$ = semi-vertical angle.
$\Rightarrow α = \frac{{sin}^{- 1} 1}{3}$
at $l = 3 r$
$\frac{d^{2} Z}{d r^{2}} = \frac{S}{9} (2 S - 24 π r^{2})$
$\frac{2 S}{9} (π r^{2} + π r l - 12 π r^{2})$
$= π r \cdot \frac{2 S}{9} (l - 11 r)$
$= \frac{2 S π r}{9} (- 8 r) < 0$
Therefore, Z is maximum.
$\Rightarrow V^{2}$ is maximum.
$\Rightarrow$ V is maximum.
Therefore, for maximum volume, semi-vertical angle $= \frac{{sin}^{- 1} 1}{3}$ .

Updated on:21/07/2023

|

Class 12 MATHS APPLICATION OF DERIVATIVES

Topper's Solved these Questions

Similar Questions

NAGEEN PRAKASHAN ENGLISH-APPLICATIONS OF DERIVATIVES-Exercise 6.5

Home
Ask Doubt
Profile