Show that the sum of the three altitudes of a triangle is less than the sum of three sides of the triangle.
Video Solution
Text Solution
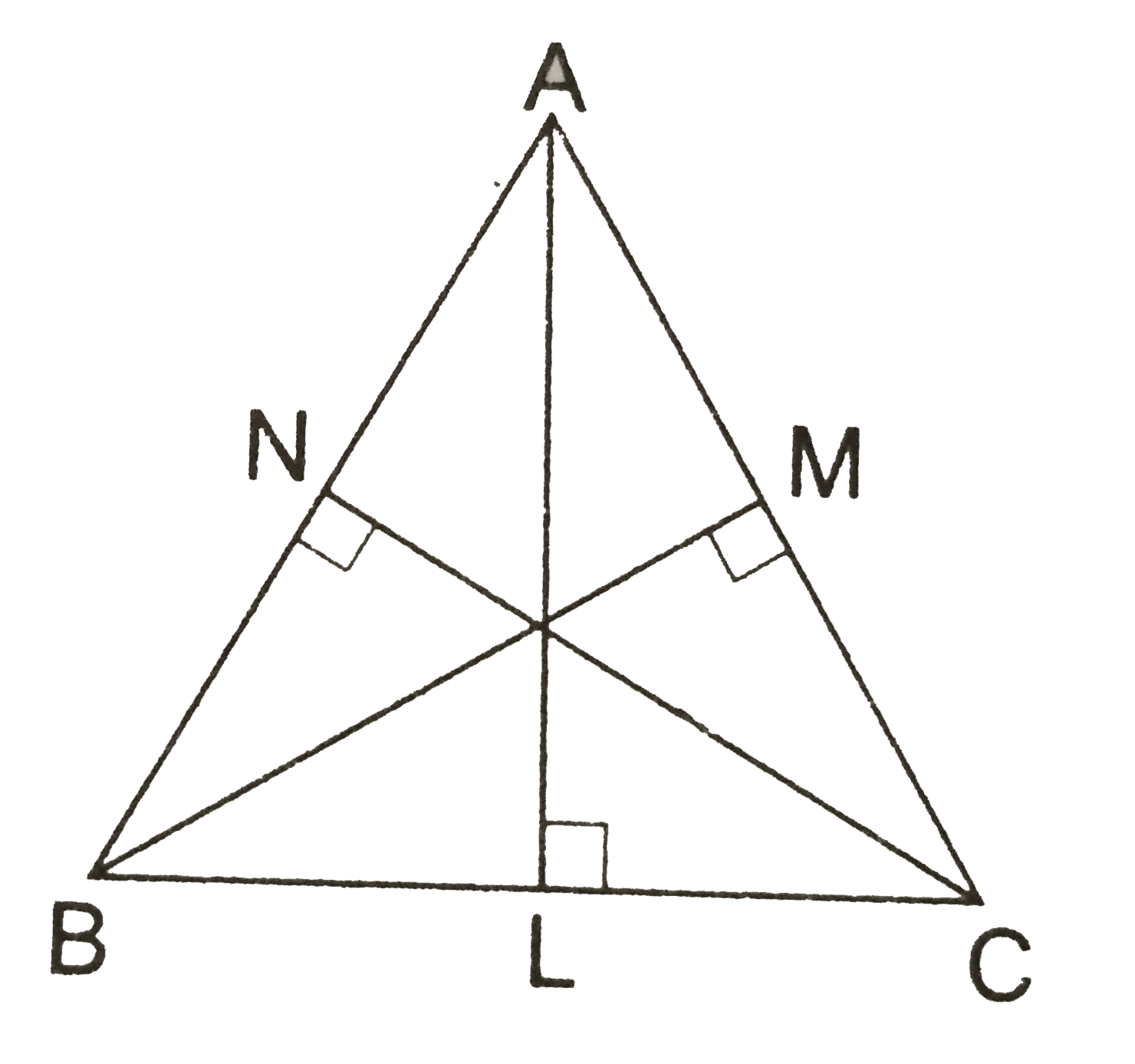
Let AL, BM, CN be the three altitudes of ΔABC.
We know that, of all line segments drawn from a point outside a line to the line, the perpendicular is the shortest.
∴ AL<AB,BM<BCandCN<AC.
∴ AL+BM+CN<AB+BC+AC.
|
Topper's Solved these Questions
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Exercise 9A
27 Videos
- CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEBOOK - RS AGGARWALCHAPTER - CONGRUENCE OF TRIANGLES AND INEQUALITIES IN A TRIANGLEEXERCISE - Exercise 9B
16 Videos
- CIRCLES BOOK - RS AGGARWALCHAPTER - CIRCLES EXERCISE - MULTIPLE CHOICE QUESTION(MCQ)
37 Videos
- COORDINATE GEOMETRYBOOK - RS AGGARWALCHAPTER - COORDINATE GEOMETRYEXERCISE - Multiple Choice Questions (Mcq)
22 Videos
Similar Questions
Knowledge Check
The sum of three altitudes of a triangle is
Aequal to the sum of three sidesBless than the sum of sidesCgreater then the sum of sidesDtwice the sum of sides.The sum of three altitudes of a triangle is
Aequal to the sum of three sidesBless than the sum of sidesCgreater than the sum of sidesDtwice the sum of sidesIf each angle of a triangle is less than the sum of the other two, then the triangle is
Aobtuse angledBright angledCacute angledDequilateral
Prove that the sum of the three angles of a triangle is 1800.
View SolutionSum of any two sides of a triangle is not less than the third side
View SolutionCan the sum of the two angles of a triangle be less than the third angles?
View SolutionIf the altitudes of a triangle are in AP, then the sides of the triangle are in
View SolutionIf the altitudes of a triangle are in A.P,then the sides of the triangle are in
View Solution
