Solve the cryptarithm: ON+ ON=GO
To solve the cryptarithm ON+ON=GO, we can break it down step by step.
Step 1: Understand the equation
We have:
ON+ON=GO
This can be rewritten as:
2×ON=GO
Step 2: Define the variables
Let:
- O be the first digit of the two-digit number ON.
- N be the second digit of the two-digit number ON.
- G be the first digit of the two-digit number GO.
Step 3: Express ON and GO in terms of O and N
The two-digit number ON can be expressed as:
ON=10O+N
And the two-digit number GO can be expressed as:
GO=10G+O
Step 4: Substitute into the equation
Substituting these expressions into our equation gives:
2×(10O+N)=10G+O
This simplifies to:
20O+2N=10G+O
Step 5: Rearrange the equation
Rearranging the equation, we get:
20O−O+2N=10G
This simplifies to:
19O+2N=10G
Step 6: Analyze the possible values
Since O, N, and G are digits (0-9), we can analyze possible values for O and N:
- The maximum value for 19O must be less than or equal to 90 (since 10G must also be a two-digit number).
- Therefore, O can take values from 1 to 4 (if O were 5 or more, 19O would exceed 90).
Step 7: Test possible values for O and N
1. If O=1:
19(1)+2N=10G⟹19+2N=10G
Testing N=1 gives 19+2(1)=21 (not valid).
Testing N=2 gives 19+4=23 (not valid).
Testing N=3 gives 19+6=25 (not valid).
Testing N=4 gives 19+8=27 (not valid).
Testing N=5 gives 19+10=29 (not valid).
Testing N=6 gives 19+12=31 (not valid).
Testing N=7 gives 19+14=33 (not valid).
Testing N=8 gives 19+16=35 (not valid).
Testing N=9 gives 19+18=37 (not valid).
2. If O=2:
19(2)+2N=10G⟹38+2N=10G
Testing N=1 gives 38+2(1)=40 (valid, G=4).
Testing N=2 gives 38+4=42 (valid, G=4).
Testing N=3 gives 38+6=44 (valid, G=4).
Testing N=4 gives 38+8=46 (valid, G=4).
Testing N=5 gives 38+10=48 (valid, G=4).
Testing N=6 gives 38+12=50 (valid, G=5).
Testing N=7 gives 38+14=52 (valid, G=5).
Testing N=8 gives 38+16=54 (valid, G=5).
Testing N=9 gives 38+18=56 (valid, G=5).
3. If O=3:
19(3)+2N=10G⟹57+2N=10G
Testing N=1 gives 57+2(1)=59 (not valid).
Testing N=2 gives 57+4=61 (not valid).
Testing N=3 gives 57+6=63 (not valid).
Testing N=4 gives 57+8=65 (not valid).
Testing N=5 gives 57+10=67 (not valid).
Testing N=6 gives 57+12=69 (not valid).
Testing N=7 gives 57+14=71 (not valid).
Testing N=8 gives 57+16=73 (not valid).
Testing N=9 gives 57+18=75 (not valid).
4. If O=4:
19(4)+2N=10G⟹76+2N=10G
Testing N=1 gives 76+2(1)=78 (not valid).
Testing N=2 gives 76+4=80 (valid, G=8).
Testing N=3 gives 76+6=82 (valid, G=8).
Testing N=4 gives 76+8=84 (valid, G=8).
Testing N=5 gives 76+10=86 (valid, G=8).
Testing N=6 gives 76+12=88 (valid, G=8).
Testing N=7 gives 76+14=90 (valid, G=9).
Testing N=8 gives 76+16=92 (valid, G=9).
Testing N=9 gives 76+18=94 (valid, G=9).
Conclusion
From our analysis, we find two valid solutions:
1. O=2,N=4,G=8
2. O=1,N=1,G=2
We have:
ON+ON=GO
This can be rewritten as:
2×ON=GO
Let:
- O be the first digit of the two-digit number ON.
- N be the second digit of the two-digit number ON.
- G be the first digit of the two-digit number GO.
The two-digit number ON can be expressed as:
ON=10O+N
And the two-digit number GO can be expressed as:
GO=10G+O
Substituting these expressions into our equation gives:
2×(10O+N)=10G+O
This simplifies to:
20O+2N=10G+O
Rearranging the equation, we get:
20O−O+2N=10G
This simplifies to:
19O+2N=10G
Since O, N, and G are digits (0-9), we can analyze possible values for O and N:
- The maximum value for 19O must be less than or equal to 90 (since 10G must also be a two-digit number).
- Therefore, O can take values from 1 to 4 (if O were 5 or more, 19O would exceed 90).
1. If O=1:
19(1)+2N=10G⟹19+2N=10G
Testing N=1 gives 19+2(1)=21 (not valid).
Testing N=2 gives 19+4=23 (not valid).
Testing N=3 gives 19+6=25 (not valid).
Testing N=4 gives 19+8=27 (not valid).
Testing N=5 gives 19+10=29 (not valid).
Testing N=6 gives 19+12=31 (not valid).
Testing N=7 gives 19+14=33 (not valid).
Testing N=8 gives 19+16=35 (not valid).
Testing N=9 gives 19+18=37 (not valid).
19(2)+2N=10G⟹38+2N=10G
Testing N=1 gives 38+2(1)=40 (valid, G=4).
Testing N=2 gives 38+4=42 (valid, G=4).
Testing N=3 gives 38+6=44 (valid, G=4).
Testing N=4 gives 38+8=46 (valid, G=4).
Testing N=5 gives 38+10=48 (valid, G=4).
Testing N=6 gives 38+12=50 (valid, G=5).
Testing N=7 gives 38+14=52 (valid, G=5).
Testing N=8 gives 38+16=54 (valid, G=5).
Testing N=9 gives 38+18=56 (valid, G=5).
19(3)+2N=10G⟹57+2N=10G
Testing N=1 gives 57+2(1)=59 (not valid).
Testing N=2 gives 57+4=61 (not valid).
Testing N=3 gives 57+6=63 (not valid).
Testing N=4 gives 57+8=65 (not valid).
Testing N=5 gives 57+10=67 (not valid).
Testing N=6 gives 57+12=69 (not valid).
Testing N=7 gives 57+14=71 (not valid).
Testing N=8 gives 57+16=73 (not valid).
Testing N=9 gives 57+18=75 (not valid).
19(4)+2N=10G⟹76+2N=10G
Testing N=1 gives 76+2(1)=78 (not valid).
Testing N=2 gives 76+4=80 (valid, G=8).
Testing N=3 gives 76+6=82 (valid, G=8).
Testing N=4 gives 76+8=84 (valid, G=8).
Testing N=5 gives 76+10=86 (valid, G=8).
Testing N=6 gives 76+12=88 (valid, G=8).
Testing N=7 gives 76+14=90 (valid, G=9).
Testing N=8 gives 76+16=92 (valid, G=9).
Testing N=9 gives 76+18=94 (valid, G=9).
From our analysis, we find two valid solutions:
1. O=2,N=4,G=8
2. O=1,N=1,G=2
Topper's Solved these Questions
Similar Questions
Solve the cryptarithm: ON+ON+ON= GO
View SolutionSolve the cryptarithm : ON+ ON+ON+ON=GO
View SolutionBy completing the following structures, adding unshared e− pairs when necessary calculate the charges
(a) N≡C−≡N
CI−C≡N
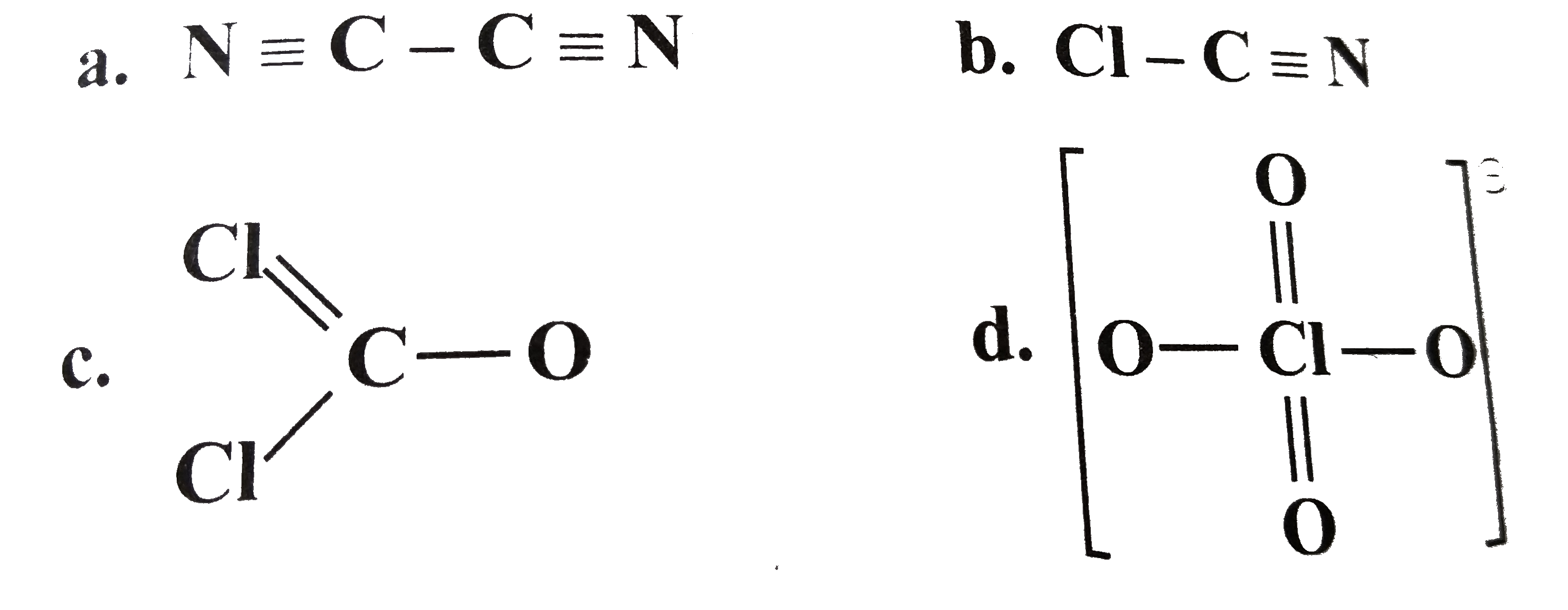
⎡⎢ ⎢⎣O−O∣∣CI∣∣O−O⎤⎥ ⎥⎦Θ
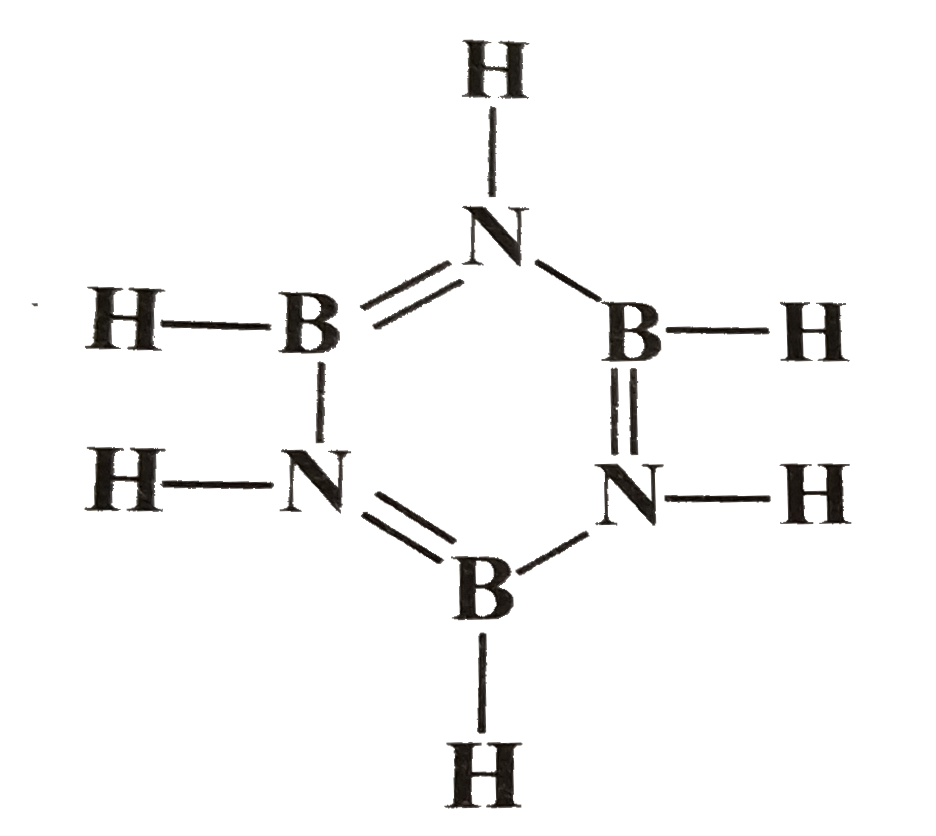 .
.
View SolutionIn Figure, lines AB, CD and EF intersect at O. Find the measures of ∠AOC, ∠COF, ∠DOE and ∠BOF .
View SolutionIn Figure, OP, OQ, OR and OS are four rays. Prove that ∠POQ+ ∠QOR+ ∠SOR+ ∠POS=3600
View SolutionLet G1,G2andG3 be the centroids of the triangular faces OBC,OCAandOAB, respectively, of a tetrahedron OABC. If V1 denotes the volumes of the tetrahedron OABCandV2 that of the parallelepiped with OG1,OG2andOG3 as three concurrent edges, then prove that 4V1=9V2.
View SolutionIn figure, AB and CD are straight lines and OP and OQ are respectively the bisectors of angles ∠BOD and ∠AOC . Show that the rays OP and OQ are in the same line.
View SolutionFor the reaction R−Br→R−O−N=O
the suitable reagent is
View SolutionIf O and O′ are circumcentre and orthocentre of ABC, then →OA+→OB+→OC equals
a.2→OO' b. →OO' c. →O'O d. 2→O'O
View SolutionThe number of oxygen atoms required to combine with 7 g of N2 to form N2O3 when 80% of N2 is converted to N2O3.
View Solution
