Solve the following linear programming problem graphically:
Minimize: z=x+3y
Subject to:
x+y≤8
3x+5y≥15
x≥0
y≥0
Draw the graph of equations x+y=8,3x+5y=15,x=0 and y=0.
Now obtain the feasible region for he inequalities x+y≤8,3x+5y≥15x≥0 and y≥0. The convex region is ABCD whose vertices are A(8,0),B(0,8),C(0,3) and D(5,0). Now we will find the value of z=x+3y at each vertex.
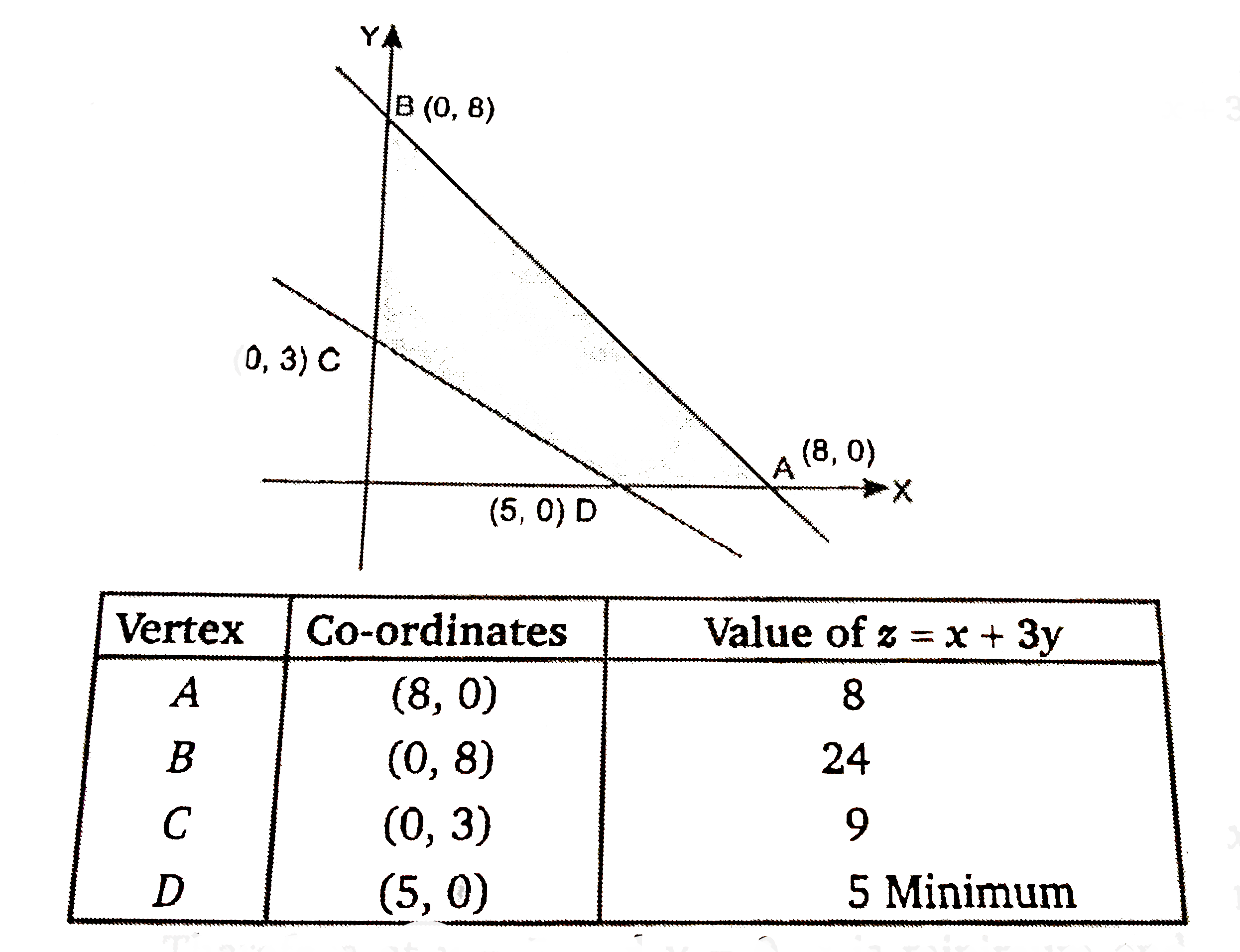
Therefore at x=5 and y=0,z is minimum and minimum value is 5.
Topper's Solved these Questions
- BOOK - NAGEEN PRAKASHANCHAPTER - LINEAR PROGRAMMINGEXERCISE - Exercise 12 A8videos
LINEAR PROGRAMMING
- BOOK - NAGEEN PRAKASHANCHAPTER - LINEAR PROGRAMMINGEXERCISE - Exercise 12 B17videos
LINEAR PROGRAMMING
- BOOK - NAGEEN PRAKASHANCHAPTER - INVERES TRIGONOMETRIC FUNCTIONSEXERCISE - Miscellaneous Exercise (prove That )9videos
INVERES TRIGONOMETRIC FUNCTIONS
- BOOK - NAGEEN PRAKASHANCHAPTER - MATRICESEXERCISE - Miscellaneous Exerice15videos
MATRICES
Similar Questions
Solve the following linear programming problem graphically:
Maximize :z=x+2y
Subject to: x−y≤2
x+y≤4
x≥0
y≥0View SolutionSolve the following linear programming problem graphically:
Maximize : z=5x+3y
Subject to:
x+3y≤5
x+y≤3
x≥0
y≥0View SolutionSolve the following linear programming problem graphically:
Maximize : z=x+9y
Subject to: x+3y≤60
x+y≥10
x≤y
x≥0
y≥0View SolutionSolve the following linear programming problem graphically:
Maximize : z=3x+5y
Subject to: x+y≥2
x+3y≥3
x≥0
y≥0View SolutionSolve the following linear programming problem graphically:
Maximize : z=30x+25y
Subject to: x+h≤6
3x+2y≤15
x≥0
y≥0View SolutionSolve the following linear programming problem graphically.
Minimize :z=2x+3y−1
Subject to:
x−y≥0
−x+2y≥2
x≥3
y≤4
y≥0View SolutionSolve the following linear programming problem graphically:
Maximize : z=60x+15y
Subject to : x+y≤50
3x+y≤90
x≥0
y≥0View SolutionSolve the following linear programming problem graphically:
Maximize :z=4x+3y
Subject to: 2x+y≥40
x+2y≥50
x+y≥35
x≥0
y≥0View SolutionSolve the Following Linear Programming Problem graphically : Minimise Z=−3x+4ySubject to x+2y≤8,3x+2y≤12,x≥0,y≥0.
View SolutionSolve the following linear programming problem graphically:
Maximize : z=200x+500y
Subject to: x+2y≥10
3x+4y≤24
x≥0
y≥0View Solution

