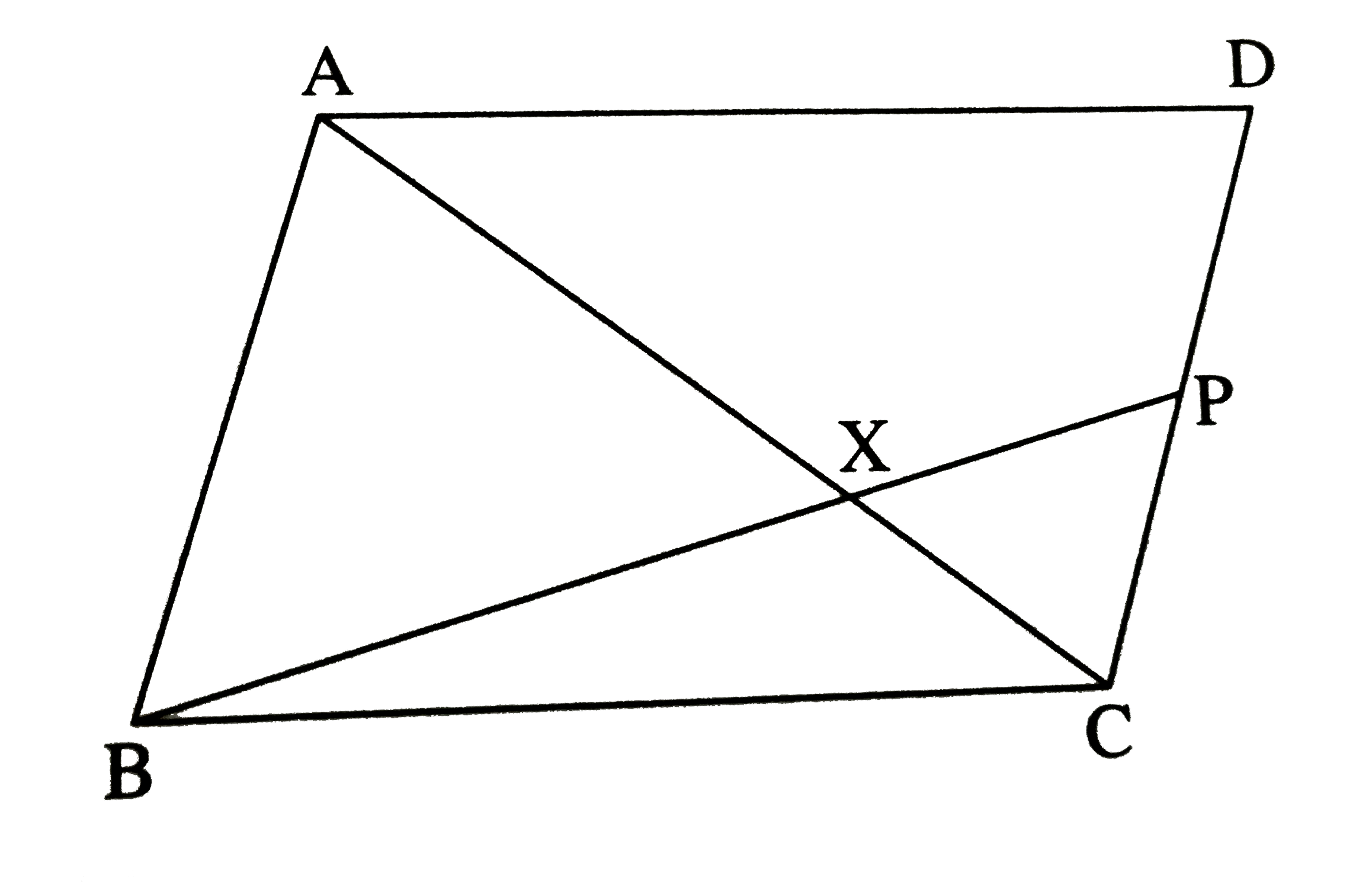
$□ A B C D$ is a parallelogram. P is any point on side BC. Find two pairs of triangles with equal areas.

Video Solution

Text Solution

Verified by Experts

The correct Answer is:i. $A (Δ A B C) = A (Δ B D C)$
ii. $A (Δ A B C) = A (Δ A B D)$

|

Answer

Step by step video & image solution for squareABCD is a parallelogram. P is any point on side BC. Find two pairs of triangles with equal areas. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.

Updated on:21/07/2023

Class 10 MATHS TRIANGLES

Topper's Solved these Questions

Similar Questions

Knowledge Check

Question 1 - Select One
ABCD is a parallelogram, E and F are the mid-points of BC and CD. Find the ratio of area of parallelogram ABCD and $Δ A E F$
A $2 : 1$
B $4 : 1$
C $8 : 3$
D $8 : 1$
Question 2 - Select One
ABCD is a parallelogram and m $∠ D A B = 30^{\circ}$ , BC=20 cm and AB=20 cm. Find the area of parallelogram:
A $150 c m^{2}$
B $200 c m^{2}$
C $400 c m^{2}$
D $260 c m^{2}$
Question 3 - Select One
The area of a parallelogram PQRS is $36 c m^{2}$ . M is any point on the side RS. The area of $Δ P M Q$ is.
A $18 c m^{2}$
B $9 c m^{2}$
C $36 c m^{2}$
D $12 c m^{2}$

TARGET PUBLICATION-SIMILARITY -Additonal Problems for Practice( Basid on Practice Set 1.1)

Home
Ask Doubt
Profile