Statement 1 : The differential equation of all circles in a
plane must be of order 3.
Statement 2 : There is only one circle passing through three
non-collinear points.
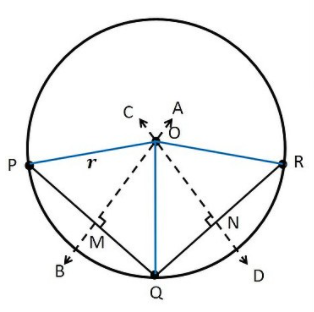
In △OPM and △OQM
OM=OM (common)
∠OMP=∠OMQ (Perpendicular angles)
PM=QM
By SAS congruency, △OPM and △OQM are congruent.
OP=OQ
Similarly, we can prove that,
OQ=OR
Thus,
OP=OQ=OR
Taking, O as center and OP as radius construct a circle. Hence circle passes through P,Q,R.
Hence points are concyclic.
Topper's Solved these Questions
- NCERT THEOREMSBOOK - NCERT ENGLISHCHAPTER - NCERT THEOREMSEXERCISE - THEOREM 10.6
1 Video
- NCERT THEOREMSBOOK - NCERT ENGLISHCHAPTER - NCERT THEOREMSEXERCISE - THEOREM 10.7
1 Video
- NCERT THEOREMSBOOK - NCERT ENGLISHCHAPTER - NCERT THEOREMSEXERCISE - THEOREM 10.4
1 Video
- LINES AND ANGLESBOOK - NCERT ENGLISHCHAPTER - LINES AND ANGLESEXERCISE - Exercise 6.1
6 Videos
- NUMBER SYSTEMSBOOK - NCERT ENGLISHCHAPTER - NUMBER SYSTEMSEXERCISE - EXERCISE 1.4
2 Videos
Similar Questions
Statement-1: The differential equation of all circles in a plane must be of order 3.Statement-2: The differential equation of family of curve y=asinx+bcos(x+c), where a,b,c are parameters is 2. (A) Both 1 and 2 are true and 2 is the correct explanation of 1 (B) Both 1 and 2 are true and 2 is not correct explanation of 1 (C) 1 is true but 2 is false (D) 1 is false but 2 is true
View SolutionSTATEMENT-1 : The differential equation of all circles in a plane can be of order 3.
and
STATEMENT-2 : General equation of a circle in plane has three independent constant parameters
View SolutionWrite the order of the differential equation of all non horizontal lines in a plane.
View SolutionThe locus of the centres of all circles passing through two fixed points.
View SolutionThe centre of circle passing through three non collinear points A,B,C is the concurrent point of
View SolutionStatement 1 : The center of the circle having x+y=3 and x−y=1 as its normals is (1, 2) Statement 2 : The normals to the circle always pass through its center
View SolutionFind the differential equation of all the circles which pass through the origin and whose centres lie on y-axis.
View SolutionThe length of the perpendicular from the origin to the plane passing though three non-collinear points →a,→b,→c is
View SolutionThe length of the perpendicular from the origin to the plane passing though three non-collinear points →a,→b,→c is
View SolutionThrough three collinear points a circle can be draw.
View Solution