Suppose S1 and S2 are two unequal circles, AB and CD are the direct common tangents to these circles. A transverse common tangent PQ cuts AB in R and CD in S. If AB = 10, then RS is -
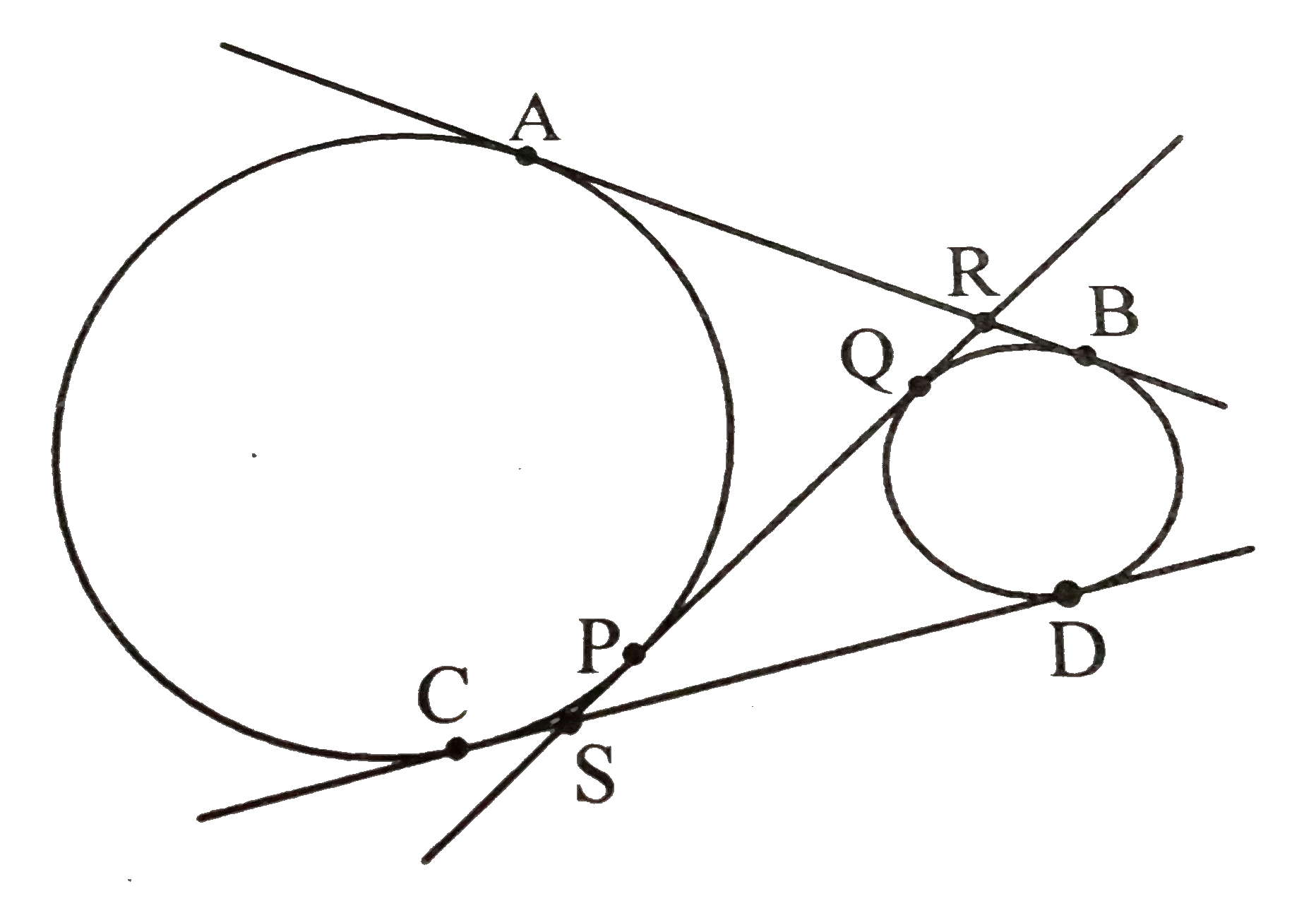
A
8
B
9
C
10
D
11
Video Solution
Text Solution
The correct Answer is:C
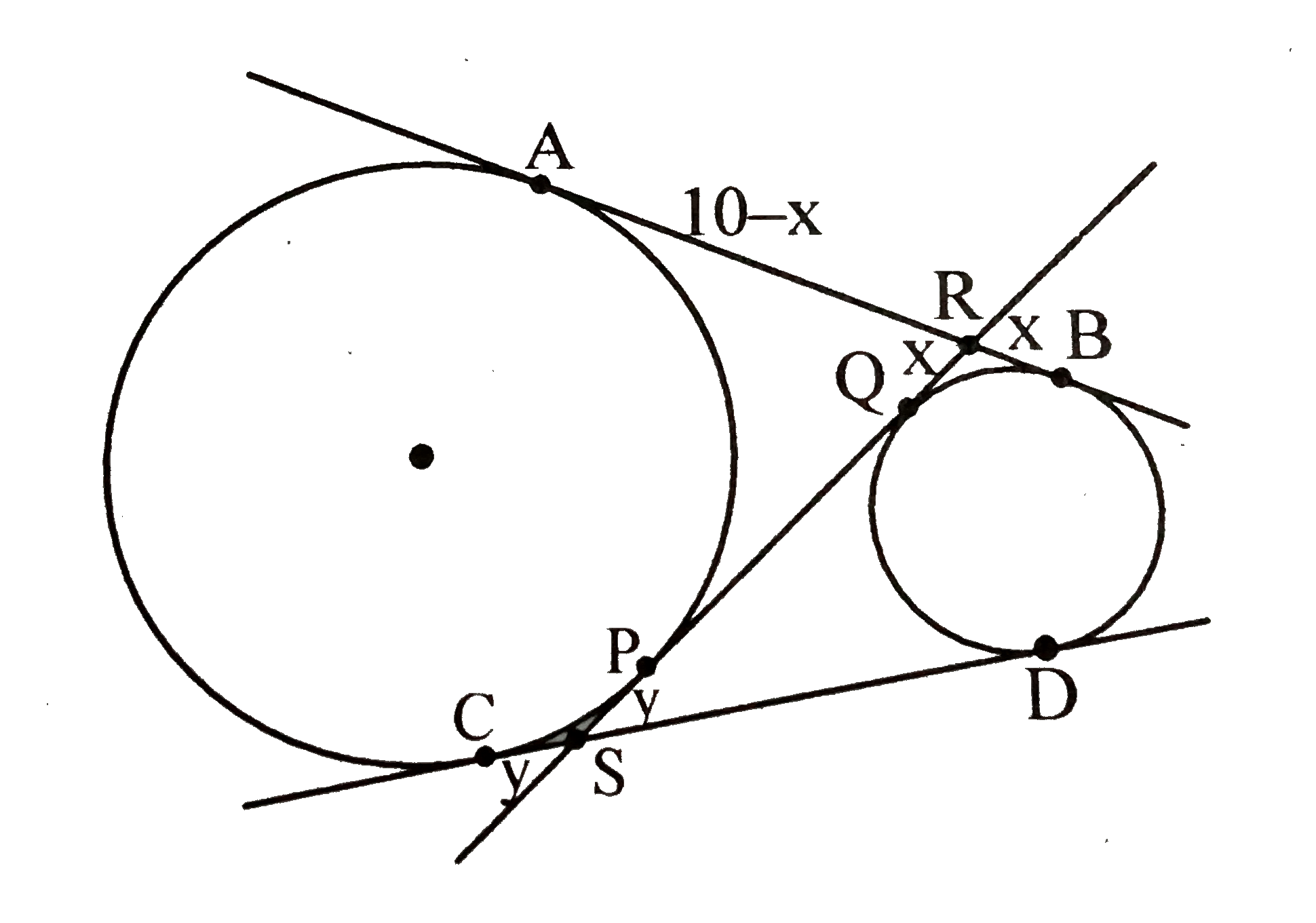
AR=PR=10−x ltBRgt PQ=10−2x
AB=CD=10
CD=CS+SD=y+SD
=y+SP+PQ
10=y+y+10−2x
RaRy=x
Now RS=SP+PQ+QR
=y+10−2x+x
=10+y−x=10
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
CD is direct common tangent to two circles intersecting each other at A and B. The ∠CAD+∠CBD is equal to
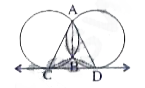 A120∘B90∘C360∘D180∘
A120∘B90∘C360∘D180∘
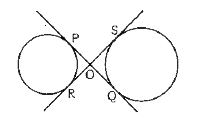
In the figure, PQ and RS are the common tangents to two circles intersecting at O.
Prove that PQ=RS
View SolutionIn figure, AB and CD are common tangents to two circles of unequal radii. Prove that AB=CD

View SolutionIn figure, AB and CD are common tangents to two circles of equal radii. Prove that AB=CD.

View SolutionCommon tangents AB and CD to two circles intersects at E. Prove that AB=CD
View SolutionIn figure, common tangents AB and CD to two circles intersect at E. Prove that AB=CD.

View SolutionAB and CD are common tangents to two circles which intersect each other at C as shown in the figure IF AB = 6cm , find CD.

View SolutionCD is direct common tangent to two circles intersecting each other at A and B. The ∠CAD+∠CBD is equal to

View Solution
