In the figure, PQ and RS are the common tangents to two circles intersecting at O.
Prove that PQ=RS
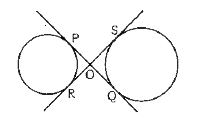
The correct Answer is:PQ=RS
Step by step video, text & image solution for In the figure, PQ and RS are the common tangents to two circles intersecting at O. Prove that PQ=RS by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Topper's Solved these Questions
- BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 7EXERCISE - PART - B (SECTION - V)8videos
SAMPLE PAPER 7
- BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 7EXERCISE - PART - B (SECTION - III)16videos
SAMPLE PAPER 7
- BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 6EXERCISE - SECTION- C10videos
SAMPLE PAPER 6
- BOOK - EDUCART PUBLICATIONCHAPTER - SAMPLE PAPER 8EXERCISE - PART - B (SECTION - V)4videos
SAMPLE PAPER 8
Similar Questions
Knowledge Check
- Question 1 - Select One
Suppose S1 and S2 are two unequal circles, AB and CD are the direct common tangents to these circles. A transverse common tangent PQ cuts AB in R and CD in S. If AB = 10, then RS is -
 A8B9C10D11
A8B9C10D11
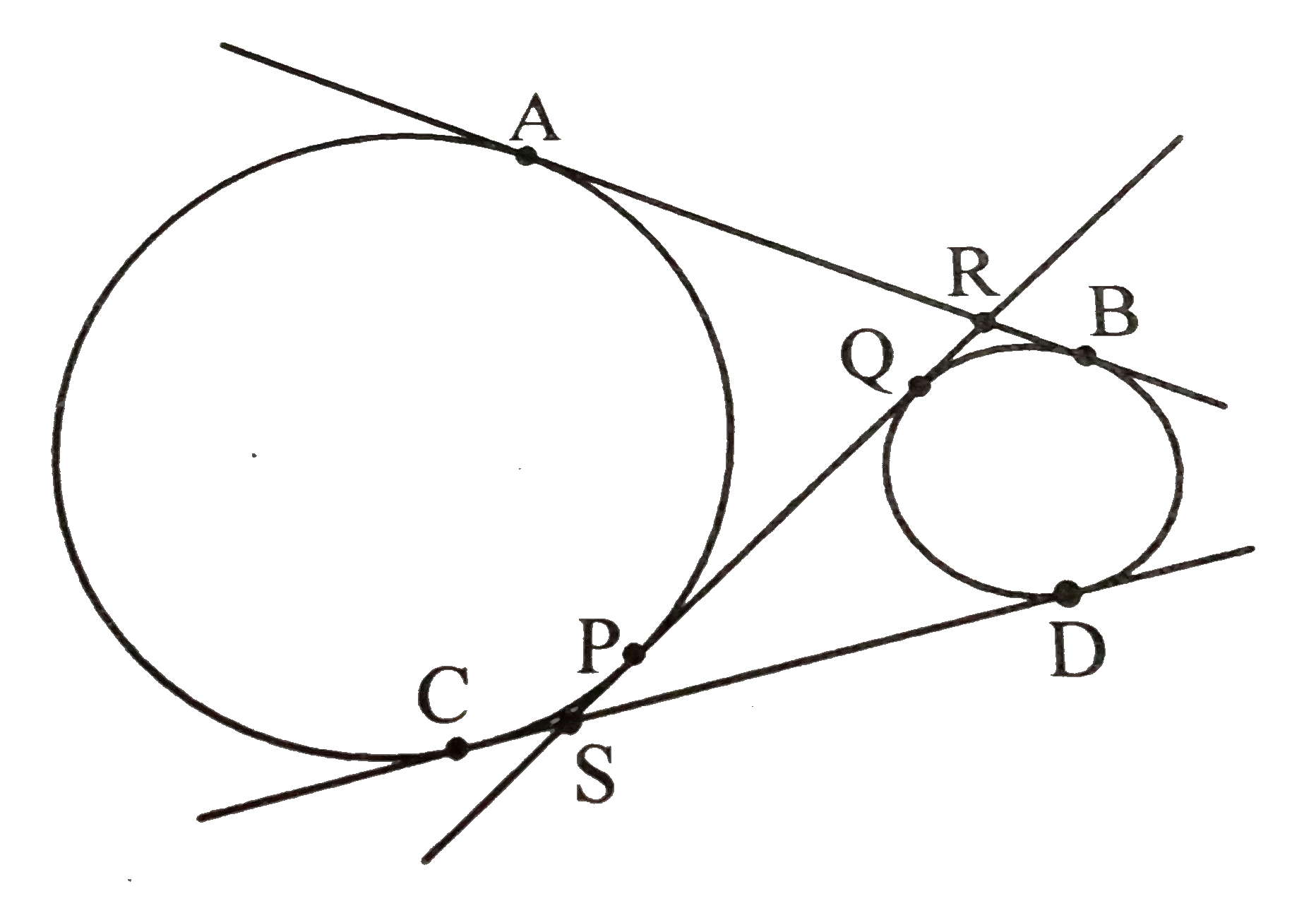
In figure, common tangents AB and CD to two circles intersect at E. Prove that AB=CD.
 View Solution
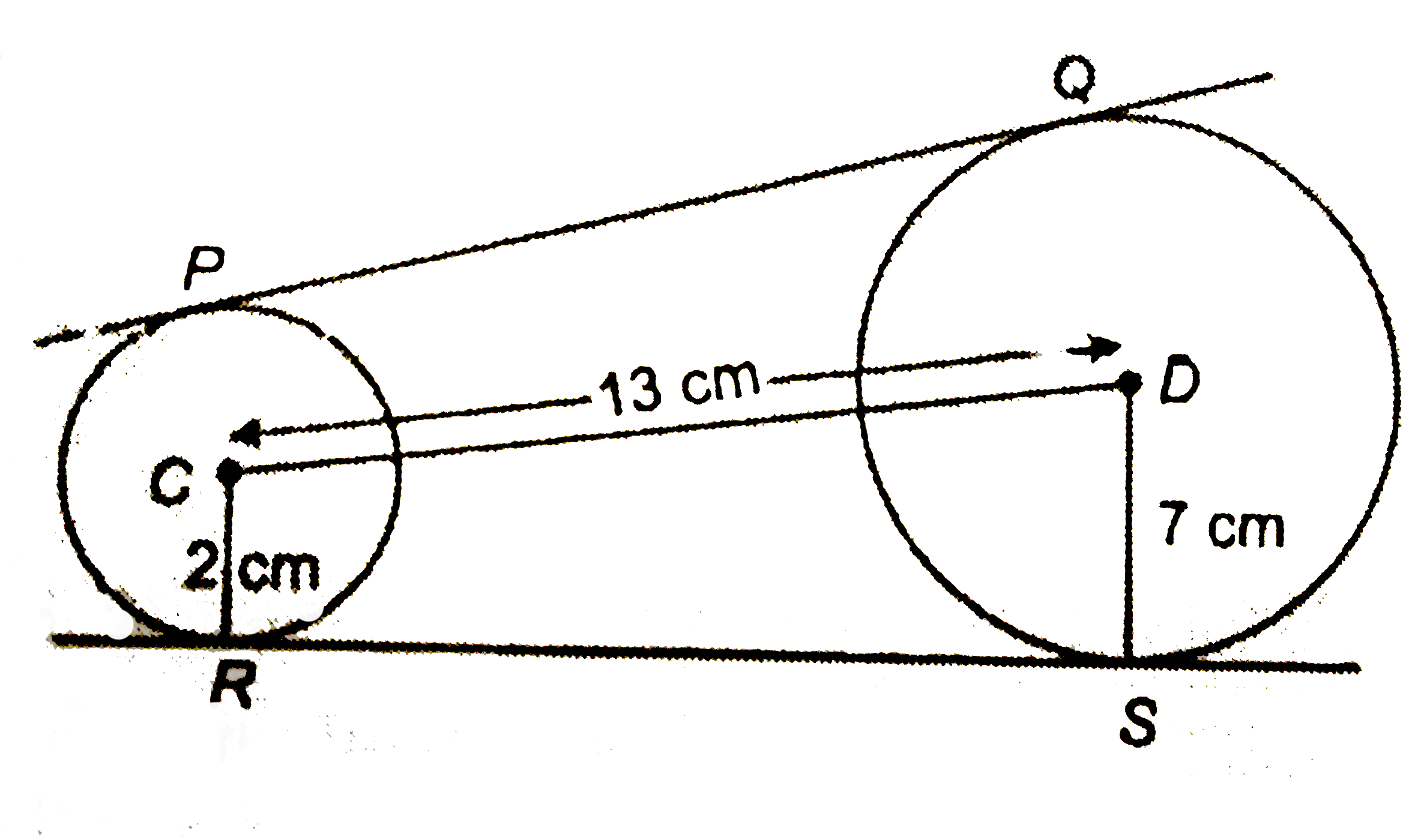
View SolutionIn the given diagram, PQ and RS are common tangents to the two circles with centres C and D. Find the length of PQ and hence area of trapexium RSDC.
 View Solution
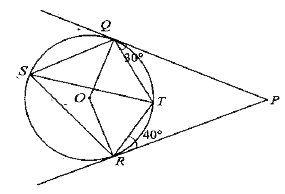
View SolutionIn the figures, PQ and PR are tangents to the circle with centre O. Find RSQ , RTQ , and RˆPQ
 View Solution
View SolutionPQ and RS are common tangents of two circles intersection at A and B. AB, when produced both sides, meet the tangents PQ and RS at x and y, respectively. If AB = 3 cm, xy = 5 cm, then PQ (in cm) will be.
View SolutionIn a figure the common tangents, AB and CD to two circles with centers O and O' intersect at E. Prove that the points O, E and O' are collinear.
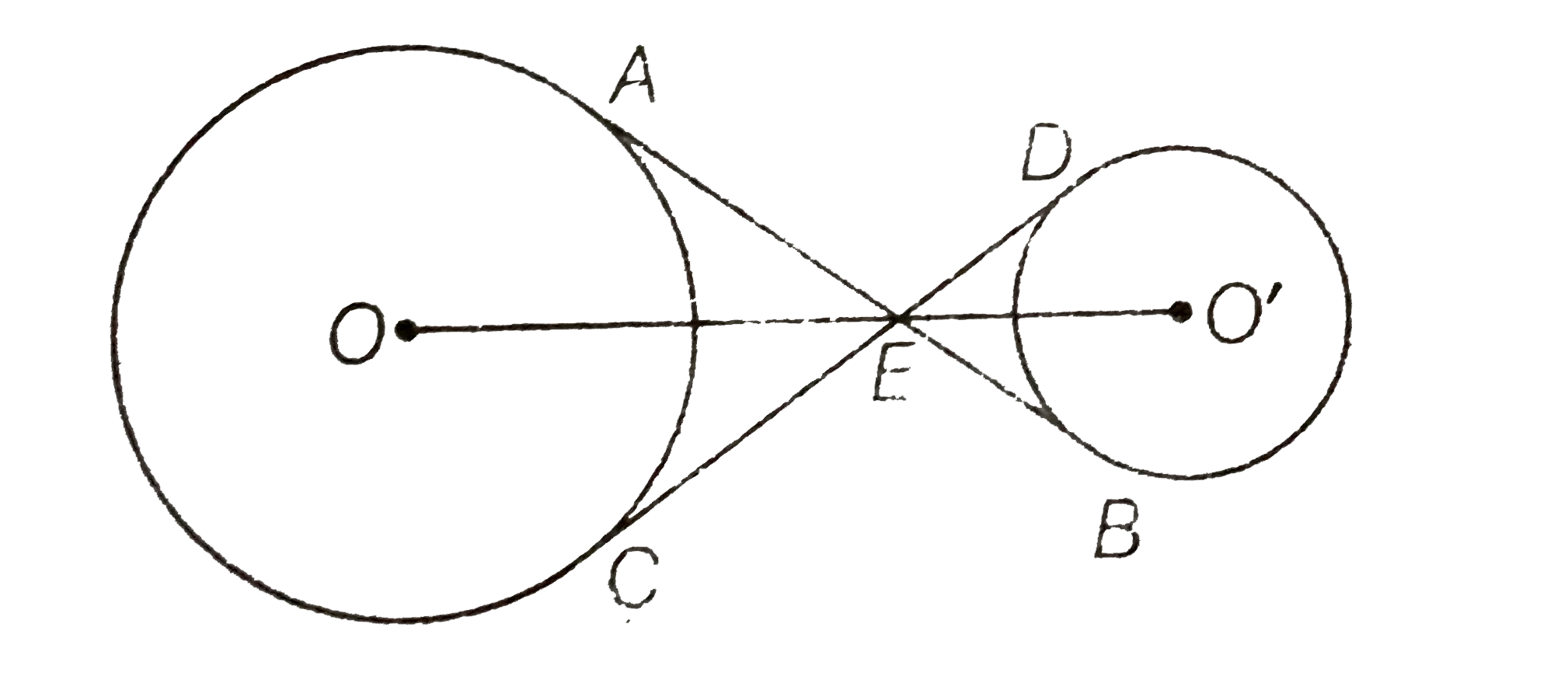 View Solution
View SolutionIn figure, PQ and PR are two tangents to a circle with centre O. IF ∠QPR=46∘ , then ∠QOR equals
 View Solution
View SolutionIn figure, two circles intersect each other at points S and R. Their common tangent PQ touches the circle at points P,Q. Prove that, ∠PRQ+∠PSQ=180∘.
 View Solution
View Solution


