Tangents PA and PB are drawn to the circle from the point P on the curve , where A and B lie on the circle. Consider the function represented by the locus of the center of the circumcircle of triangle PAB. Then answer the following questions.
The period of is
not defined
The correct Answer is:3
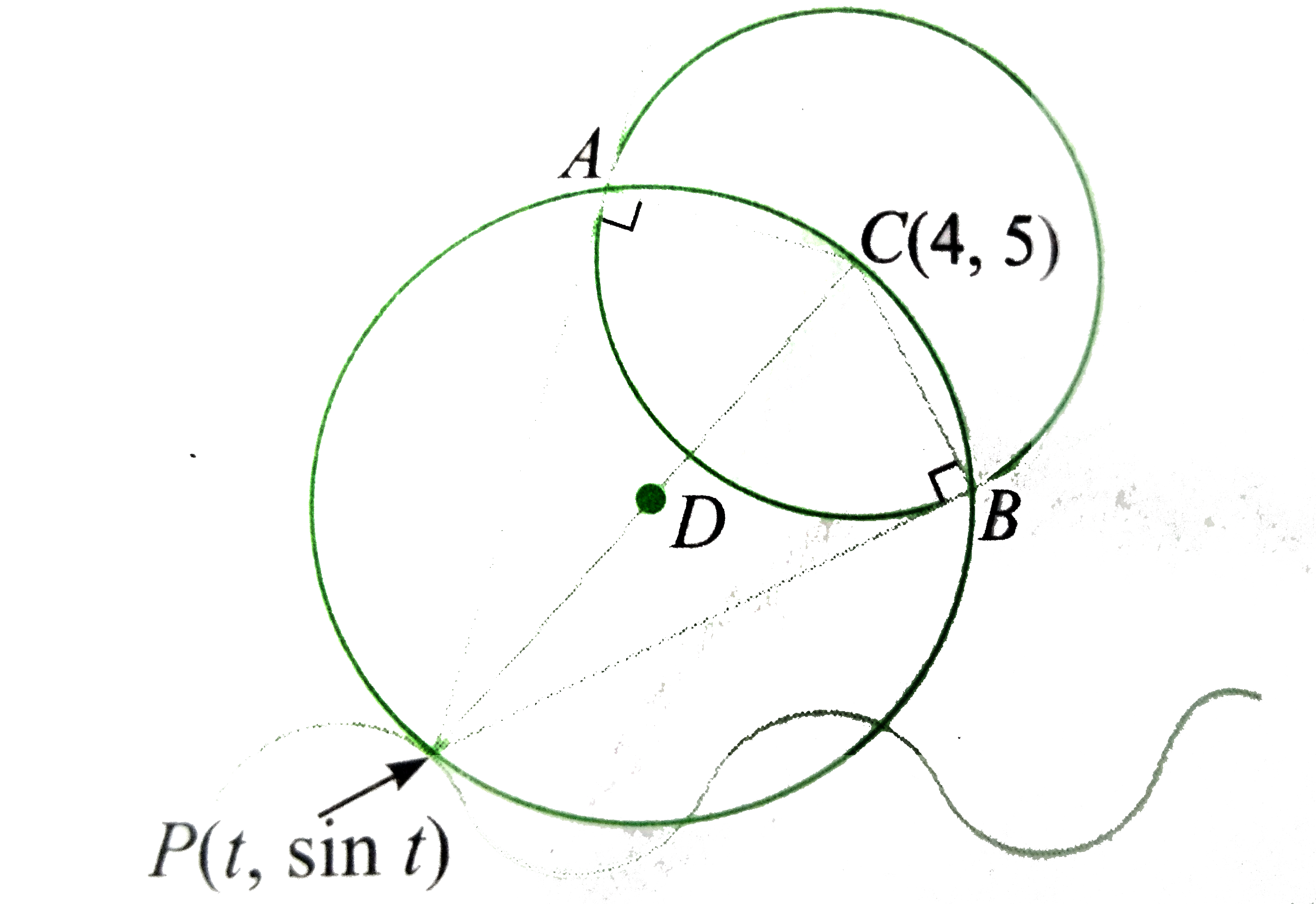
The center of the given circle is . Points P,A,C, and B are concyclic such that PC is the diameter of the circle. Hence, the center D(h,k) of the circumcircle of is the midpoint of PC.
Then, we have
and
Eliminating t, we have
or
Thus, the range of
is and the priod is .
Al,so , i.e.., which has no real solutions.
For which has no real solutions.
But range of is
Topper's Solved these Questions
- CIRCLE Book:CENGAGEChapter:CIRCLE Exercise:MATRIX MATCH TYPE
Explore 6 Videos
- CIRCLE Book:CENGAGEChapter:CIRCLE Exercise:Exercise (Matrix)
Explore 1 Video
- CIRCLE Book:CENGAGEChapter:CIRCLE Exercise:Exercise (Multiple)
Explore 25 Videos
- BINOMIAL THEORMBook:CENGAGEChapter:BINOMIAL THEORMExercise:Question Bank
Explore 31 Videos
- CIRCLESBook:CENGAGEChapter:CIRCLESExercise:Question Bank
Explore 32 Videos
Similar Questions
Tangents PA and PB are drawn to the circle (x−4)2+(y−5)2=4 from the point P on the curvey=sinx , where A and B lie on the circle. Consider the function y=f(x) represented by the locus of the center of the circumcircle of triangle PAB. Then answer the following questions.
Which of the following is true ?
View SolutionTangents PA and PB are drawn to the circle (x+3)2+(y−4)2=1 from a variable point P on y=sinx. Find the locus of the centre of the circle circumscribing triangle PAB.
View Solution
Knowledge Check
Tangents PA and PB are drawn to the circle (x−4)2+(y−5)2=4 from the point P on the curvey=sinx , where A and B lie on the circle. Consider the function y=f(x) represented by the locus of the center of the circumcircle of triangle PAB. Then answer the following questions.
The range of y=f(x) isA[−2,1]B[−1,4]C[0,2]D[2,3]Tangents PA and PB are drawn to the circle (x−4)2+(y−5)2=4 from the point P on the curvey=sinx , where A and B lie on the circle. Consider the function y=f(x) represented by the locus of the center of the circumcircle of triangle PAB. Then answer the following questions.
Which of the following is true ?Af(x)=4 has real roots.Bf(x)=1 has real roots.CThe range of y=f−1 is [−π4+2,π4+2]DNone of theseTangents PA and PB are drawn to x2+y2=4 from the point P(3,0). Area of triangle PAB is equal to:-
A109√5 sq. unitsB203√5 sq. unitsC59√5 sq. unitsDNone of these
Tangents PA and PB are drawn to the circle x2+y2=4,then locus of the point P if PAB is an equilateral triangle ,is equal to
View SolutionTangents PA and PB are drawn to x2+y2=4 from the point P(3,0). Area of triangle PAB is equal to:-
View SolutionTangents PAandPB are drawn to the circle x2+y2=8 from any arbitrary point P on the line x+y=4. The locus of mid-point of chord of contact AB is
View SolutionTangents PA and PB are drawn to the circle x2+y2=4,then locus of the point P if PAB is an equilateral triangle ,is equal to
View SolutionTangents PAandPB are drawn to the circle x2+y2=8 from any arbitrary point P on the line x+y=4. The locus of mid-point of chord of contact AB is
View Solution
