The angle bisectors of a parallelogram form a rectangle.
AD||BC and AB is traversal
∠A+∠B=180∘
12∠A+12∠B=90∘
∠BAS+∠ABS=90∘
In∠ABS
∠BAS+∠ABS+∠ASB=180∘
90∘+∠ASB=180∘
∠ASB=90∘
∠RSP=90∘
∠SRB=90∘
∠RQP=90∘
∠SPQ=90∘.
Topper's Solved these Questions
Similar Questions
Show that the bisectors of angles of a parallelogram form a rectangle.
View SolutionShow that the bisectors of angles of a parallelogram form a rectangle.
View Solution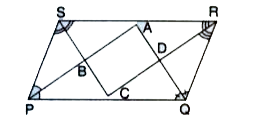
In the alongside diagram, the bisectors of interior angles of the parallelogram PQRS enclose a quadrilateral ABCD.
Show that:
(i) ∠PSB+∠SPB=90∘
(ii) ∠PBS=90∘
(iii) ∠ABC=90∘
(iv) ∠ADC=90∘
(v) ∠A=90∘
(vi) ABCD is a rectangle
thus, the bisectors of the angles of a parallelogram enclose a rectangle.View SolutionProve that the quadrilateral formed by the bisectors of the angles of a parallelogram is a rectangle.
 View Solution
View SolutionProve that the quadrilateral formed by the bisectors of the angles of a parallelogram is a rectangle.
 View Solution
View SolutionThe figure formed by joining the mid-point of the adjacent sides of a parallelogram is a (a)rectangle (b) parallelogram (c) rhombus (d) square
View SolutionShow that, in a parallelogram ABCD, the internal and external bisectors of ∠Aand∠B from a rectangle.
View SolutionIf the two diagonals of a parallelogram are equal, it is a rectangle.
View SolutionProve that the bisectors of opposite angles of a parallelogram are parallel.
View SolutionThe opposite angles of a parallelogram are equal.
View Solution

