The area bounded by the loop of the curve 4y2=x2(4−x2) is given by (1) 73 (2) 83 (3) 113 (4) 163
A
7/3 sq. units
B
8/3 sq. units
C
11/3 sq. units
D
16/3 sq. units
Video Solution
Text Solution
The correct Answer is:D
4y2=x2(4−x2) (1)
or y=±12√x2(4−x2)
=±x2√(4−x2)
⇒ y=−x2√(4−x2),
y=x2√(4−x2)
y=−x2√(4−x2), y=x2√(4−x2)
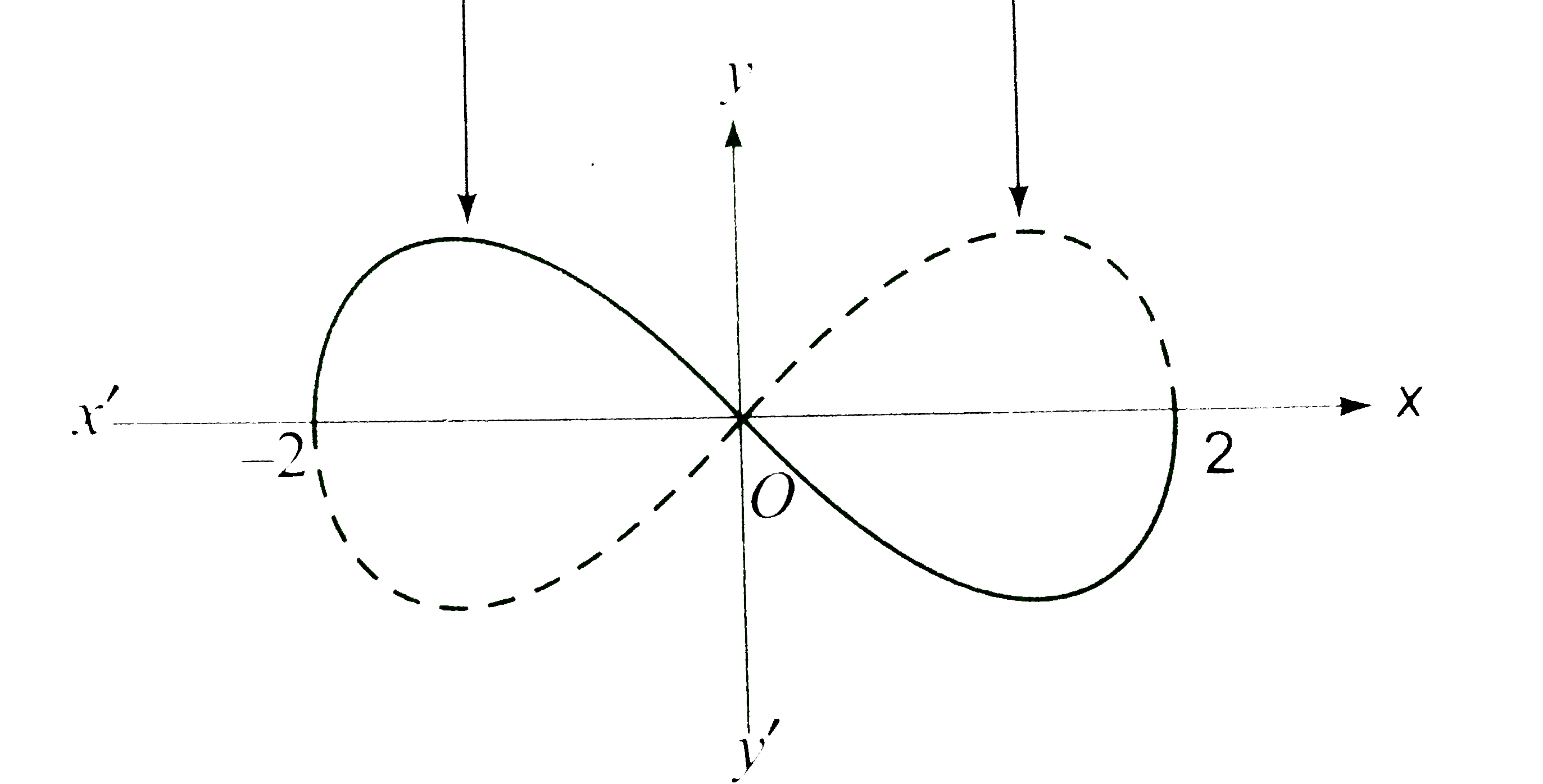
∴ Area (A)=4×∫20x2√(4−x2)dx
Let 4−x2=t⇒−2xdx=dt
⇒ A=∫40√tdt=[t3/23/2]=23x[√64−0]
=163 sq. units
|
Topper's Solved these Questions
- AREABOOK - CENGAGE ENGLISHCHAPTER - AREAEXERCISE - Multiple Correct Answers Type
13 Videos
- AREABOOK - CENGAGE ENGLISHCHAPTER - AREAEXERCISE - Linkded Comprehension Type
21 Videos
- AREABOOK - CENGAGE ENGLISHCHAPTER - AREAEXERCISE - Concept Application Exercise 9.3
7 Videos
- APPLICATIONS OF DERIVATIVESBOOK - CENGAGE ENGLISHCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Comprehension Type
5 Videos
- BINOMIAL THEOREMBOOK - CENGAGE ENGLISHCHAPTER - BINOMIAL THEOREMEXERCISE - Matrix
4 Videos
Similar Questions
The area bounded by the X-axis and the curve y=4x−x2−3 is
View SolutionThe area bounded by the x-axis and the curve y=4x−x2−3 is
View SolutionThe area bounded by the loop of the curve 4y2=x2(4−x2) is (a)7/3 sq. units (b) 83sq.unites 113sq.units (d) 163sq.units
View SolutionFind the area bounded by the curve 4y2=9xand3x2=16y
View SolutionThe area bounded by the curve y=3|x|andy+|2−x|=2 is
View SolutionFind the area bounded by the curve x2=y,x2=−yandy2=4x−3
View SolutionArea bounded by the curves y=x2−1andx+y=3 is:
View SolutionFind the area bounded by the curve y=x3−3x2+2x and the x-axis.
View SolutionThe area induced between the curves y=x24a and y=8a3x2+4a2 is given by
View SolutionThe area bounded by the curve y2=4x and the line 2x−3y+4=0 is
View Solution
