The area enclosed by the curves is
A
sq. units
B
sq. units
C
sq. units
D
None of these
Video Solution
Text Solution
The correct Answer is:A
The two curves are
Curve (1) is symmetrical about x-axis and have y-axis as the asympote.
Curve (2) is symmetrical about x-axis, tangent at origin as y-axis, and the asymptote x=a.
The two curves intersect at the point
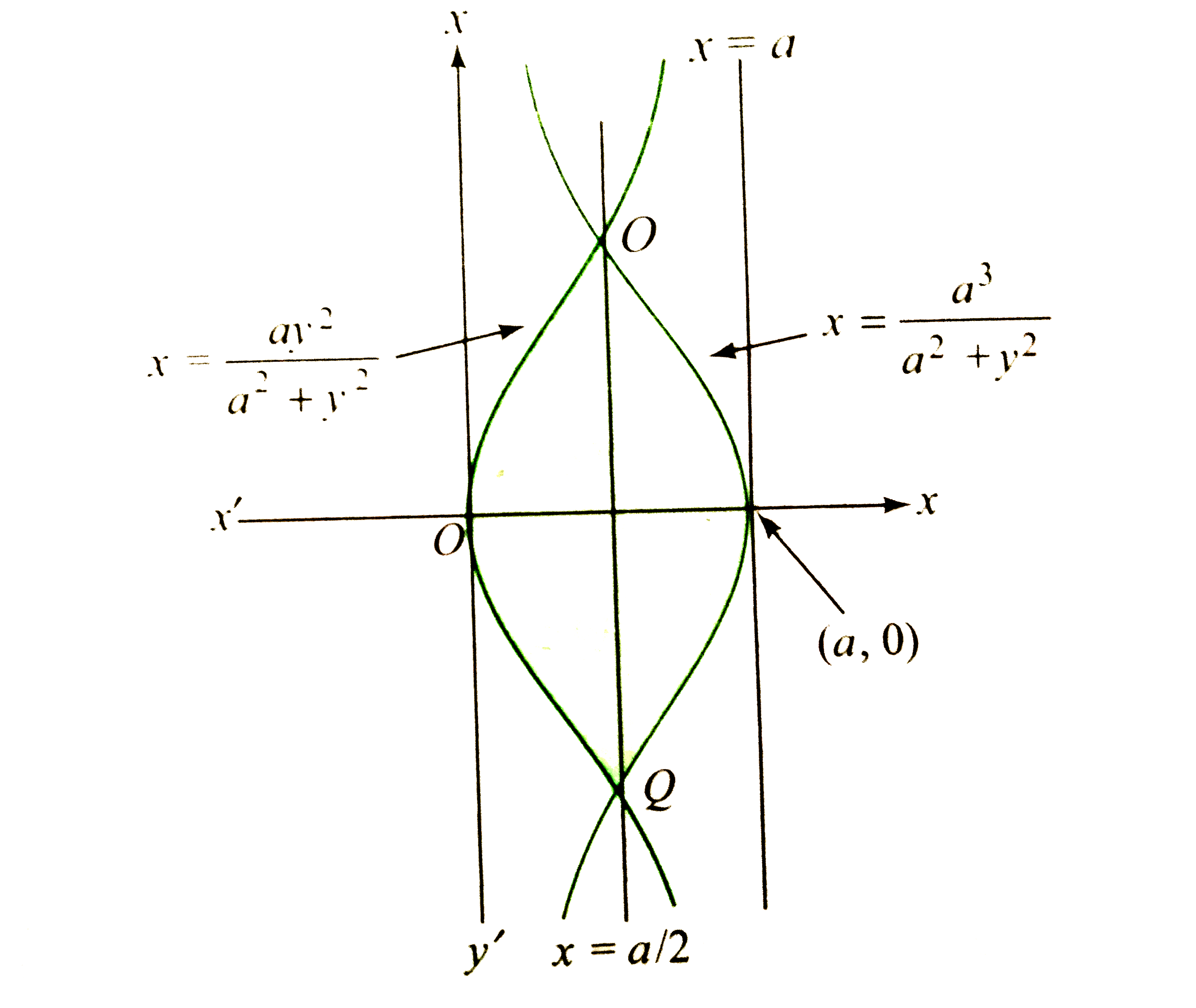
(integrating along y-axis)
sq. units.
|
Topper's Solved these Questions
- AREABOOK - CENGAGE ENGLISHCHAPTER - AREAEXERCISE - Multiple Correct Answers Type
13 Videos
- AREABOOK - CENGAGE ENGLISHCHAPTER - AREAEXERCISE - Linkded Comprehension Type
21 Videos
- AREABOOK - CENGAGE ENGLISHCHAPTER - AREAEXERCISE - Concept Application Exercise 9.3
7 Videos
- APPLICATIONS OF DERIVATIVESBOOK - CENGAGE ENGLISHCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Comprehension Type
5 Videos
- BINOMIAL THEOREMBOOK - CENGAGE ENGLISHCHAPTER - BINOMIAL THEOREMEXERCISE - Matrix
4 Videos
Similar Questions
The area enclosed by the curves xy2=a2(a−x) and (a−x)y2=a2x is
View SolutionThe area enclosed by the curve y2+x4=x2 is
View SolutionFind the area enclosed by the curves x^2=y , y=x+2,
View SolutionThe area enclosed between the curves y2=xandy=|x| is
View SolutionFind the area enclosed by the curves y=4x2 and y2=2x.
View SolutionFind the area enclosed by the curve y=3x and y=6x-x2
View SolutionShow that the area enclosed between the curve y2=12(x+3)andy2=20(5−x) is 64√53
View SolutionFind the area enclosed by the curves 3x2+5y=32andy=|x−2|.
View SolutionIf the area enclosed between the curves y=ax2andx=ay2(a>0) is 1 square unit, then find the value of a.
View SolutionFind the area enclosed between the curves
y=x2,y=2x−x2
View Solution
