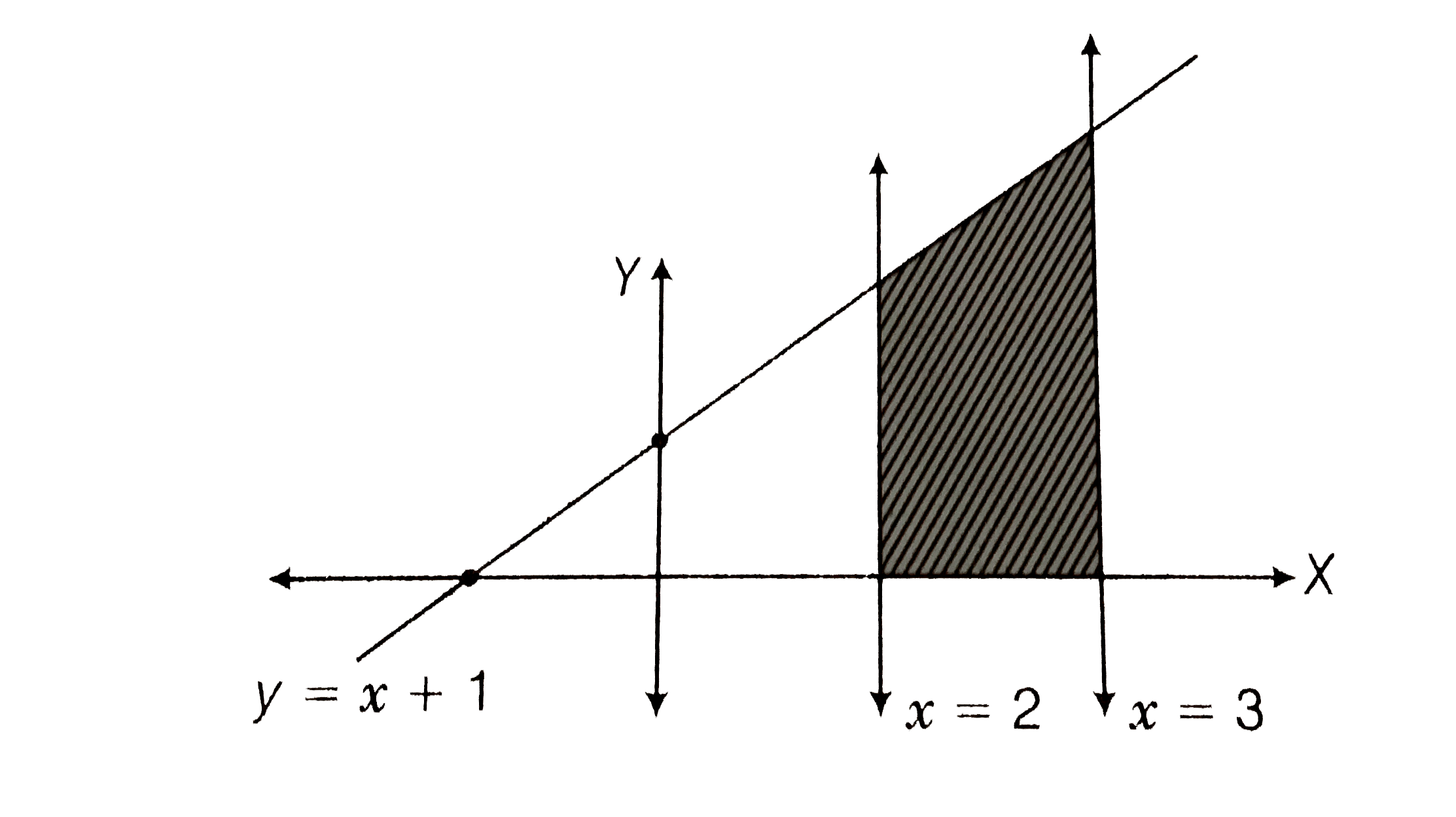
The area of the region bounded by the curve y = x + 1 and the lines x=2,x=3, is
72sq units
92 sq unit
112 sq unit
132 sq units
Required area, A=∫32(x+1)dx=[x22+x]32
=[92+3−42−2]=[52+1]=72 sq units
Topper's Solved these Questions
- APPLICATION OF INTEGRALSBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - APPLICATION OF INTEGRALSEXERCISE - Long Answer Type Questions
16 Videos
- APPLICATION OF DERIVATIVESBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - APPLICATION OF DERIVATIVESEXERCISE - Fillers
5 Videos
- CONTINUITY AND DIFFERENTIABILITYBOOK - NCERT EXEMPLAR ENGLISHCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - True/False
10 Videos
Similar Questions
The area of the region bounded by the curve y=|x−1| and y=1 is:
View SolutionThe area of the region bounded by the curves y=xex,y=ex and the lines x=±1, is equal to
View SolutionFind the area of the region bounded by the curve y2=xand the lines x=1,x=4and the x-axis.
View SolutionThe area of the region bounded by the curve x=2y+3 and the lines y=1,y=−1 is
View SolutionFind the area of the region bounded by the curve y2=4xand the line x=3.
View SolutionThe area of the region bounded by the curve y=x3 , and the lines , y=8 and x=0, is
View SolutionThe area of the region bounded by the curve y=x2−2 and line y = 2 , is equal to
View SolutionA body weighs w Newton on the surface of the earth. Its weight at a height equal to half the radius of the earth, will be xyw where x and y are coprimes . Find x and y
View SolutionThe area of the region bounded by the curve y=ex and lines x=0 and y=e is
View SolutionThe area of the region bounded by the curve y=ex and lines x=0 and y=e is
View Solution
