Question

The area of the region containing the points $(x,y)$
satisfying $4\le x^2+y^2\le 2(\left|x\right|+\left|y\right|)$
is

(a)$8sq\stackrel{.}{u}nits$
(b) $2sq\stackrel{.}{u}nits$

(c)$4\pi sq\stackrel{.}{u}nits$
(d) $2\pi sq\stackrel{.}{u}nits$

Explanation

The points in the required region satisfy
`" "4le x^(2) + y^(2) le 2 (|x| + |y|)" "` (i)
Since curve (i) is symmetrical about both the axes, the required area is 4 times the area of the region in the first quadrant. Therefore, it is sufficient to sketch the region and to find the area in the first quadrant.
In the first quadrant, curve (i) consists of two curves :
`" "x^(2) + y^(2) ge 4 " "(C_(1))" "and x^(2)+y^(2)-2x -2y ge0" "(C_(2))`

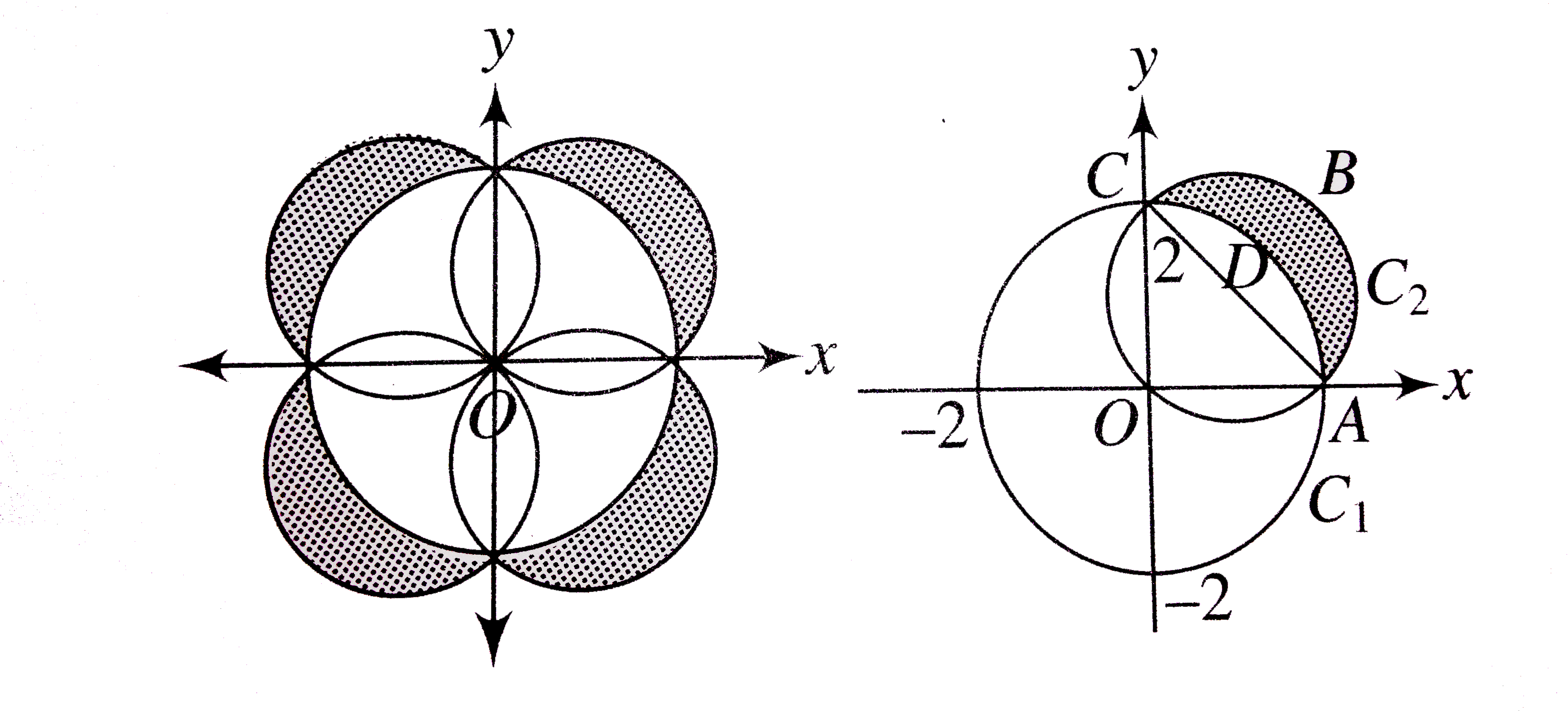
`therfore " "` Required area = 4 area ABCDA
= 4 (area of semi-circle ABCA)- (area of sector ADCA)
= 4 (area of semi-circle ABCA)-(area of sector sector OADCO- area of triangle OAC)
`= 4 {pi- (pi-2)}= 8` sq. units