The area of the region of the plane bounded by max(|x|,|y|)≤1 and xy≤12
is
(a)
12+ln2 sq. units
(b) 3+ln2 sq. units
(c)314 sq. units
(d) 1+2ln2 sq. units
1/2 + In 2 sq. units
3+ In 2 sq. units
31/4 sq. units
1+2 In 2 sq. units
The correct Answer is:B
max(|x|,|y|)≤1⇒|x|≤1and|y|≤1
which represent square bounded by x=±1andy=±1
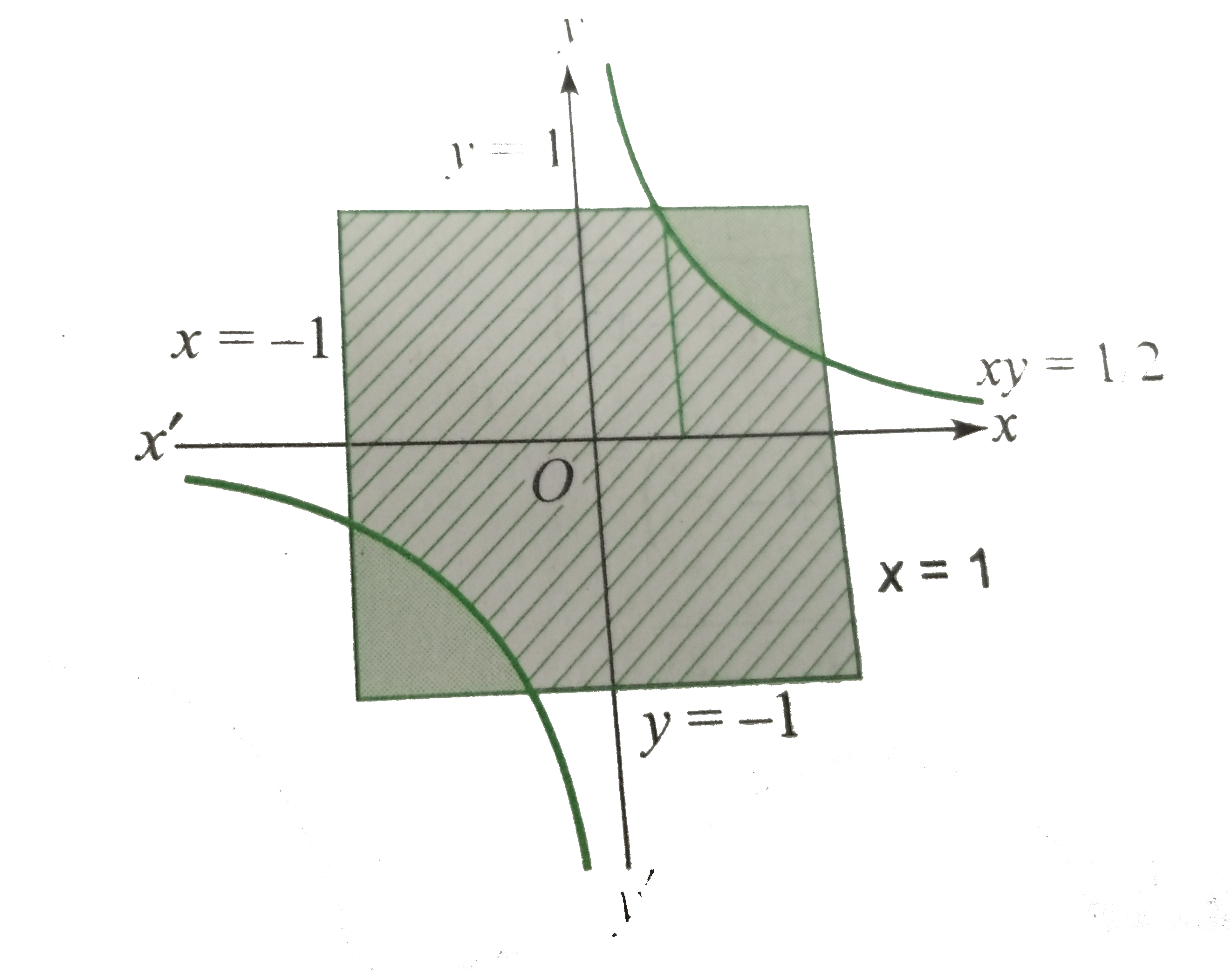
The required area is the lined area.
Now, shaded area is given by
21∫1/2(1−12x)dx=2(x−12 In x)1
=2[(1−0)−(12−12 In 12)]
=1− In 2 sq. units.
or Horizontal lined area =4−(1− In 2)=3+ In 2. sq. units.
Topper's Solved these Questions
- AREABOOK - CENGAGE ENGLISHCHAPTER - AREAEXERCISE - Multiple Correct Answers Type
13 Videos
- AREABOOK - CENGAGE ENGLISHCHAPTER - AREAEXERCISE - Linkded Comprehension Type
21 Videos
- AREABOOK - CENGAGE ENGLISHCHAPTER - AREAEXERCISE - Concept Application Exercise 9.3
7 Videos
- APPLICATIONS OF DERIVATIVESBOOK - CENGAGE ENGLISHCHAPTER - APPLICATIONS OF DERIVATIVESEXERCISE - Comprehension Type
5 Videos
- BINOMIAL THEOREMBOOK - CENGAGE ENGLISHCHAPTER - BINOMIAL THEOREMEXERCISE - Matrix
4 Videos
Similar Questions
The area of the region bounded by x=0,y=0,x=2,y=2,y≤ex and y≥1nx is (a) 6−41n2sq.units (b) 41n2−2sq.units 21n2−4sq.units (d) 6−21n2sq.units
View SolutionThe area of the closed figure bounded by x=−1,x=2,and y={−x2+2,x≤12x−1,x>1and the ascissa axis is (a)163sq.units (b) 103sq.units (c)133sq.units (d) 73sq.units
View SolutionConsider two curves C1:y2=4[√y]xandC2:x2=4[√x]y, where [.] denotes the greatest integer function. Then the area of region enclosed by these two curves within the square formed by the lines x=1,y=1,x=4,y=4 is (a)83sq.units (b) 103sq.units (c)113sq.units (d) 114sq.units
View SolutionThe area of the smaller region bounded by circle x2+y2=1 and |y|=x+1 (a)π2−12sq.units (b) π2−1sq.units (c) π2sq.units (d) π2+1sq.units
View SolutionThe area of the closed figure bounded by y=x22−2x+2 and the tangents to it at (1,12)and(4,2) is 98sq.units (b) 38sq.units 32sq.units (d) 94sq.units
View SolutionThe area of the region whose boundaries are defined by the curves y=2cosx,y=3tanx and the y-axis is (a) 1+31n(2√3)sq.units (b)1+321n3−31n2sq.units (c)1+321n3−1n2sq.units (d)1n3−1n2sq.units
View SolutionThe area bounded by the curves y=xex,y=xe−x and the line x=1 is 2esq.units (b) 1−2esq.units 1esq.units (d) 1−1esq.units
View SolutionThe area of the region containing the points (x,y) satisfying 4≤x2+y2≤2(|x|+|y|) is (a)8sq.units (b) 2sq.units (c)4πsq.units (d) 2πsq.units
View SolutionLet f(x)=x3+3x+2andg(x) be the inverse of it. Then the area bounded by g(x) , the x-axis, and the ordinate at x=−2andx=6 is (a) 94sq.units (b) 43sq.units (c) 54sq.units (d) 73sq.units
View SolutionThe area bounded by the curve a2y=x2(x+a) and the x-axis is a23sq.units (b) a24sq.units 3a24sq.units (d) a212sq.units
View Solution
