The circumference of a circle circumscribing an equilateral triangle is 24πunits. Find the area of the circle inscribed in the equilateral triangle.Solution in Bengali
The correct Answer is:36π sq. unit
In the figure, circumcircle of equilateral triangle ABC has circumference 24π.
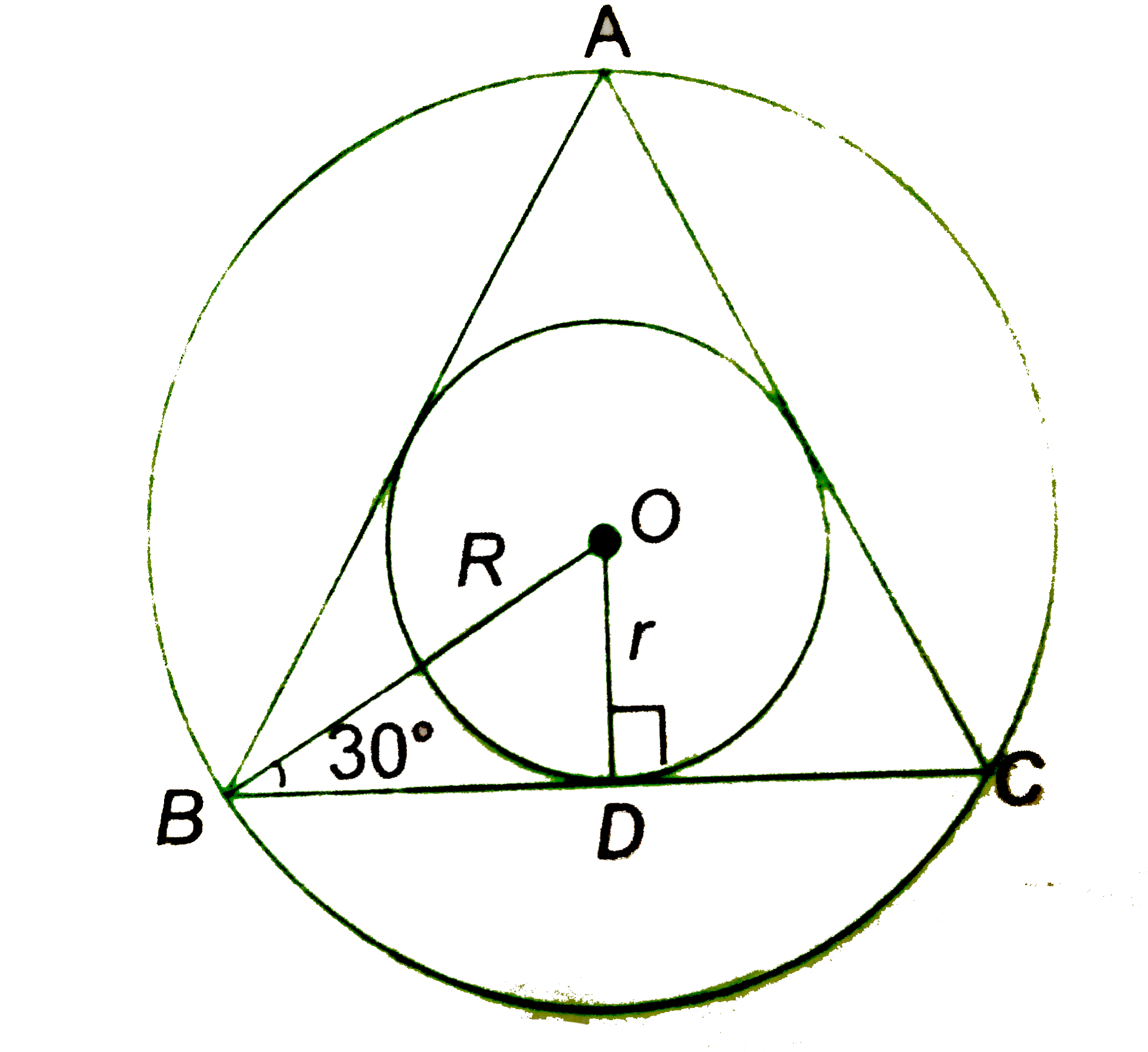
Let R be the radius of the circle and O be the centre.
∴2πR=24π
⇒R=12
Circle inscribed in triangle touches BC at D, which is midpoint of BC.
In triangle ODB, sin30∘=ODOB=rR (r is the radius of incircle)
∴r=122=6
∴ Area of inscrived circle =πr2=36π sq. unit
Topper's Solved these Questions
- TRIGONOMETRIC FUNCTIONS Book:CENGAGE PUBLICATIONChapter:TRIGONOMETRIC FUNCTIONS Exercise:Concept Application Exercises 2.2
Explore 8 Videos
- TRIGONOMETRIC FUNCTIONS Book:CENGAGE PUBLICATIONChapter:TRIGONOMETRIC FUNCTIONS Exercise:Concept Application Exercises 2.3
Explore 4 Videos
- TRIGONOMETRIC FUNCTIONS Book:CENGAGE PUBLICATIONChapter:TRIGONOMETRIC FUNCTIONS Exercise:example
Explore 10 Videos
- TRIGONOMETRIC EQUATIONSBook:CENGAGE PUBLICATIONChapter:TRIGONOMETRIC EQUATIONSExercise:Archives (Numerical value type)
Explore 4 Videos
- TRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULASBook:CENGAGE PUBLICATIONChapter:TRIGONOMETRIC RATIOS AND TRANSFORMATION FORMULASExercise:Archives (Numerical Value Type)
Explore 2 Videos
Similar Questions
Prove that sinx−cosx+1sinx+cosx−1=secx+tanx
View SolutionA horse is tied to a post by a rope. If the horse moves along a circular path always keeping the rope tight, and describes 88 metres when it traces 72∘ at the centre, find the length of the rope.
View SolutionIf 2cosx+sinx=1, then find the valie of 7x+6sinx.
View SolutionThe number of all possible values of θ, where 0<θ<π, for which the system of equations (y+z)cos3θ=(xyz)sin3θ,xsin3θ=2cos3θy+2sin3θzand(xyz)sin3θ=(y+2z)cos3θ+ysin3θ have a solution (x0,y0,z0) wiith y0z0≠0 is
View SolutionThe maximum value of the expression 1sin2θ+3sinθcosθ+5cos2θ is………
View SolutionA circle is inscribed in an equilateral triangle of side a. The area of any square inscribed in this circle is
View SolutionThe circumference of a circle circumscribing an equilateral triangle is 24πunits. Find the area of the circle inscribed in the equilateral triangle.
View SolutionThe area of an equilateral triangle inscribed in a circle of radius 4cm, is
View SolutionThe area of an equilateral triangle,inscribed in a circle is 16V3cm2. The area of the circle in terms of ? will be- -66.
View SolutionThe area of a circle inscribed in an equilateral triangle is 154cm^(2). Find the perimeter of the triangle.
View SolutionAn equilateral triangle has a circle inscribed in it and is circumscribed by a circle.There is another equilateral triangle inscribed in the inner circle.Find the ratio of the areas of the outer circle and the inner equilateral triangle.
View SolutionAn equilateral triangle has a circle inscribed in it and is circumscribed by a circle. There is another equilateral triangle inscribed in the inner circle. Find the ratio of the areas of the outer circle and the inner equilateral triangle.
View Solution
An equilateral triangle with side 12 is inscribed in a circle . Find the shaded area .
View SolutionAn equilateral triangle with a perimeter of 12 is inscribed in a circle. What is the area of circle?
View SolutionA circle is inscribed ina n equilateral triangle and a square is inscribed in the circle. The ratio of the area of the triangle to the area of the square is
View SolutionA circle is inscribed in an equilateral triangle and a square is inscribed in the circle. The ratio of the area of the triangle to the area of the square is______
View Solution