The density of a solid sphere of radius R is ρ(r)=20r2R2 where r is the distance from is center. If the gravitational field due to this sphere at a distance 4 R from its center is E and G is the gravitational constant, the ratio EGR is
π5
3π
3π2
π
The correct Answer is:D
Topper's Solved these Questions
- EAMCET - 2018 (TS) SHIFT - 2BOOK - SIA PUBLICATIONCHAPTER - EAMCET - 2018 (TS) SHIFT - 2EXERCISE - Chemistry
18 Videos
- EAMCET - 2018 (TS) SHIFT - 2BOOK - SIA PUBLICATIONCHAPTER - EAMCET - 2018 (TS) SHIFT - 2EXERCISE - Chemistry
18 Videos
- EAMCET - 2018 (TS) SHIFT - 1BOOK - SIA PUBLICATIONCHAPTER - EAMCET - 2018 (TS) SHIFT - 1EXERCISE - EXERCISE - Chemistry
8 Videos
- EAMCET -2016 (AP)BOOK - SIA PUBLICATIONCHAPTER - EAMCET -2016 (AP)EXERCISE - CHEMISTRY
3 Videos
Similar Questions
Charge density of a sphere of radius R is ρ=ρ0r where r is distance from centre of sphere.Total charge of sphere will be

View SolutionThe density inside a solid sphere of radius a is given by ρ=ρ0r, where ρ0 is the density at the surface and r denotes the distance from the centre. Find the gravitational field due to this sphere at a distance 2a from its centre.
View Solution
Knowledge Check
Charge density of a sphere of radius R is ρ=ρ0r where r is distance from centre of sphere.Total charge of sphere will be
 AρπeR2B2ρ0πeR2C3ρ0πeR2D4ρ0πeR2
AρπeR2B2ρ0πeR2C3ρ0πeR2D4ρ0πeR2A hallow metal sphere of radius R is uniformly charged. The electric field due to the sphere at a distance r from the centre:
Adecreases as r increases for r<R and r>RBincreases as r increases for r<R and r>RCzero as r increases for r<R, decreases as r increases for r>RDzero as r increases for r<R, increases for r>R
The density inside a solid sphere of radius a is given by ρ=ρ0r, where ρ0 is the density ast the surface and r denotes the distance from the centre. Find the graittional field due to this sphere at a distance 2a from its centre.
View SolutionThe density inside a solid sphere of radius a is given by ρ=ρ0r, where ρ0 is the density ast the surface and r denotes the distance from the centre. Find the graittional field due to this sphere at a distance 2a from its centre.
View SolutionThe density inside a solid sphere of radius a is given by ρ=ρ0(1−ra), where ρ0 is the density at the surface and r denotes the distance from the centre. Find the gravitational field due to this sphere at a distance 2a from its centre.
View SolutionA hallow metal sphere of radius R is uniformly charged. The electric field due to the sphere at a distance r from the centre:
View SolutionThe volume charge density of a sphere carrying charge Q and of radius R is proportional to the square of the distance from the centre. The ratio of the magnitude of the electric field at a distance 2R from the centre to that at a distance of R2 from the centre is
View SolutionMass density of sphere having radius R varies as ρ=ρ0(1−r2R2) . Find maxium magnitude of gravitational field
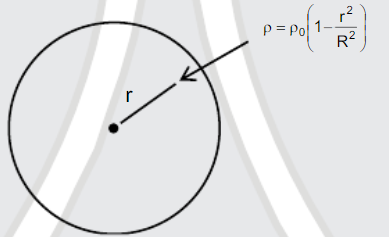
View Solution
