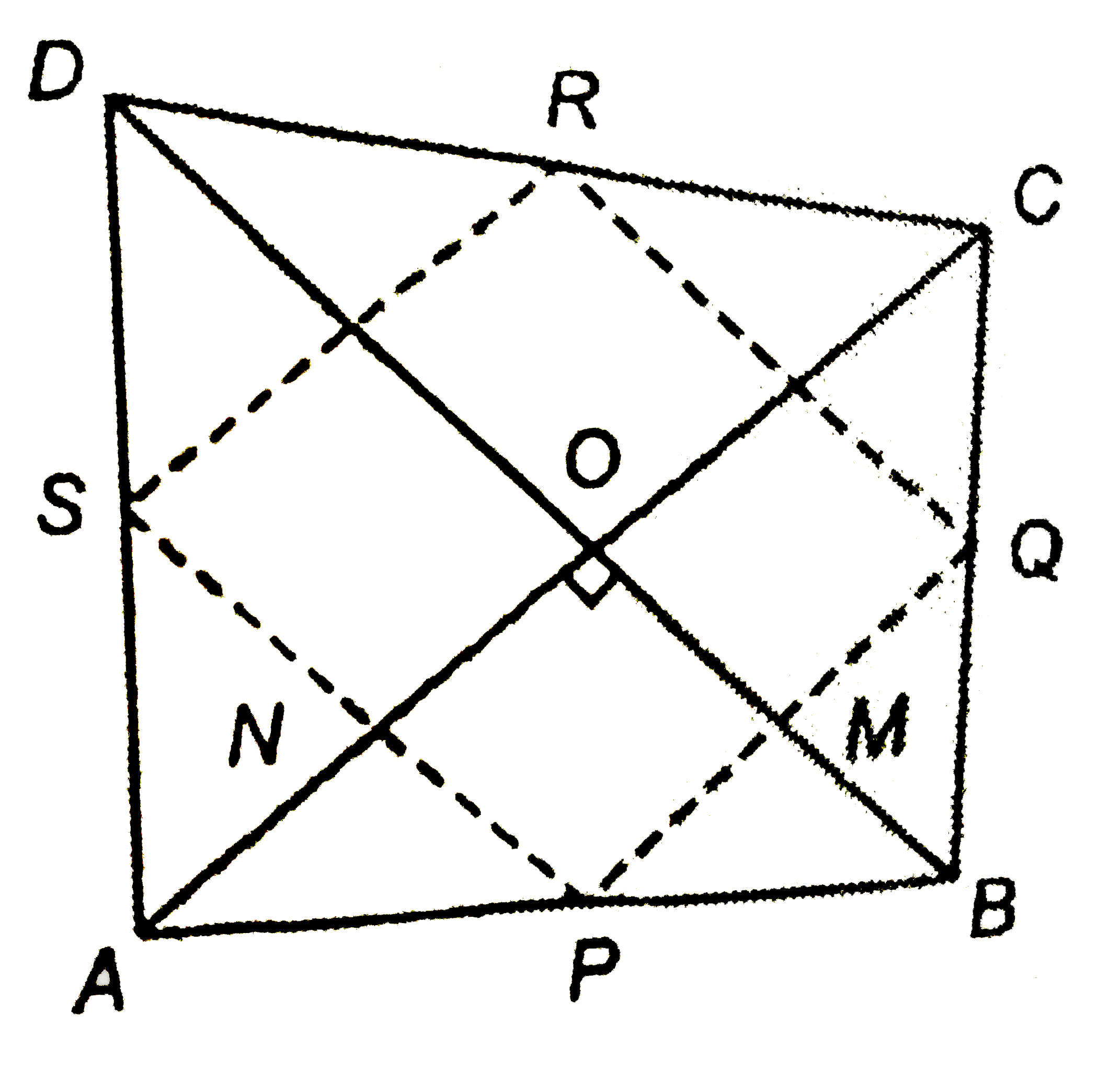
The diagonals of a quadrilateral ABCD are perpendicular. Show that the quadrilateral, formed by joining the mid-points of its sides, is a rectangle.
To prove-PQRS is a rectangle
Proof-
In∠ABC,PQ||AC and PQ=1/2AC
In∠ADC SR||AC and SR=1/2AC
In PQRS PQ=SR,PQRS is a parallelogram
PS||BO and PN||NO
PQ||AC and PM||QN
PMON is a parallelogram
∠MPN=∠MON
∠MPN=90∘
∠MPN=∠QPS=90∘
PQRS is a rectangle.
Topper's Solved these Questions
Similar Questions
The diagonals of a quadrilateral ABCD are perpendicular. Show that the quadrilateral, formed by joining the mid-points of its sides, is a rectangle.
View SolutionShow that the quadrialteral formed by joining the mid-points of the consecutive sides of a rhombus, is a rectangle.
View SolutionThe diagonals of a quadrilateral ABCD are mutually perpendicular . Prove that the quadrilateral formed by joining the mid-points of its consecutive sides is a reactangle.
 View Solution
View SolutionShow that the quadrilateral formed by joining the mid-points of the consecutive sides of a rectangle is a rhombus.
View SolutionShow that the quadrilateral formed by joining the mid-points of the consecutive sides of a rectangle is a rhombus.
View SolutionShow that the quadrilateral, formed by joining the mid-points of the sides of a square is also a square.
View SolutionShow that the quadrilateral formed by joining the mid-points of the consecutive sides of a rectangle is a rhombus.
View SolutionShow that the quadrilateral, formed by joining the mid-points of the sides of a square, is also a square.
View SolutionThe diagonals of a quadrilateral ABCD are equal. Prove that the quardilateral formed by joining the midpoints of its sides is a rhombus.
View SolutionThe quadrilateral formed by joining the mid-points of the sides AB, BC, CD, DA of a quadrilateral ABCD is
View Solution

