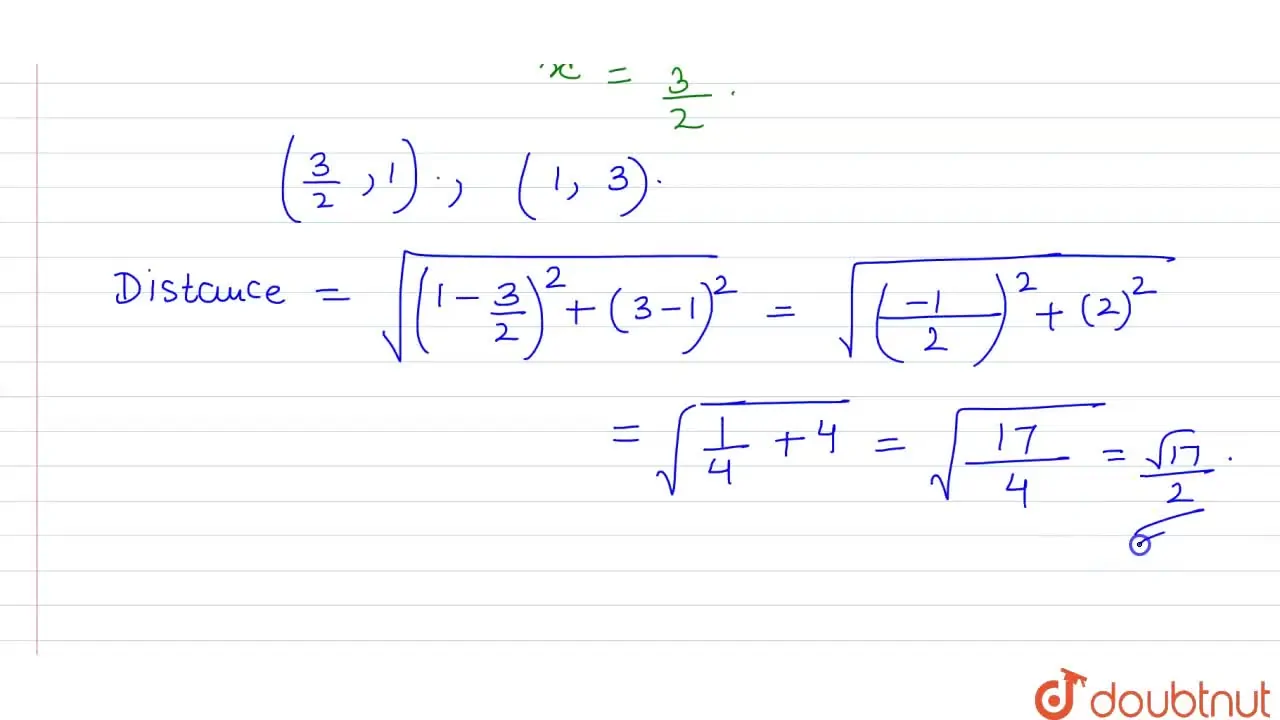The distance of the point (1, 3) from the line 2x+3y=6, measured parallel to the line 4x+y=4, is
5√13 units
3√17 unit
√17 units
√172 units
The correct Answer is:D
The line 4x+y=4 can be written as y=−4x+4.
So, slop is -4.
The line parallel to 4x+y=4 will have slope −4 only. Given point =(1,3)
Equation of line passing through (1, 3) and slope -4 is y−3=−4(x−1)
⇒y−3=−4x+4⇒4x+y=7.
Solving the two equations, we get
2x+3y=6⇒4x+6y=12
{:(4x+y=7),(cancel((-))(-) (-)),(bar(5y=5implies y=1)):}
2x+3y=6⇒2x+3(1)=6
⇒2x=3⇒x=32.
Distance between the points (1, 3) and (32,1) is
√(32−1)2+(1−3)2=√(12)2+(−2)2=√14+4=√174=√172.
Related Playlists
Similar Questions
The distance of the point (1 , 3) from the line 2x + 3y = 6 measured parallel to the line 4 x + y = 4 , is :
View SolutionThe distance of the point (3,5) from the line 2x+3y−14=0 measured parallel to the line x−2y=1 is
View SolutionThe distance of the point (2,3) from the line 3x+2y=17, measured parallel to the x-y=4 is
View SolutionFind the distance of the point (3,5) from the line 2x+3y=14 measured parallel to the line x−2y=1.
View SolutionThe distance of the point (1,–2,3) from the plane x–y+z=5 measured parallel to the line x2=y3=−z6 is :-
View SolutionFind the distance of the point (3,4,5) from the plane x+y+z=2, measured parallel to the line 2x=y=z.
View SolutionThe distance of the point (1,−2,3) from the plane x−y+z−5=0, measured parallel to the line x2=y3=z−1−6 is equal to
View SolutionFind the distance of the point(1, 0, -3) from the plane x−y−z=9 measured parallel to the line, x−22=y+23=z−6−6.
View SolutionDistance of a point (2,5) from the line 2x-y-4=0 measured parallel to the line 3x-4y + 8 = 0 is :
View SolutionThe distance of the point (1,−2,3) from the plane x−y+z=5 measured parallel to the line x2=y3=z−6, is
View Solution