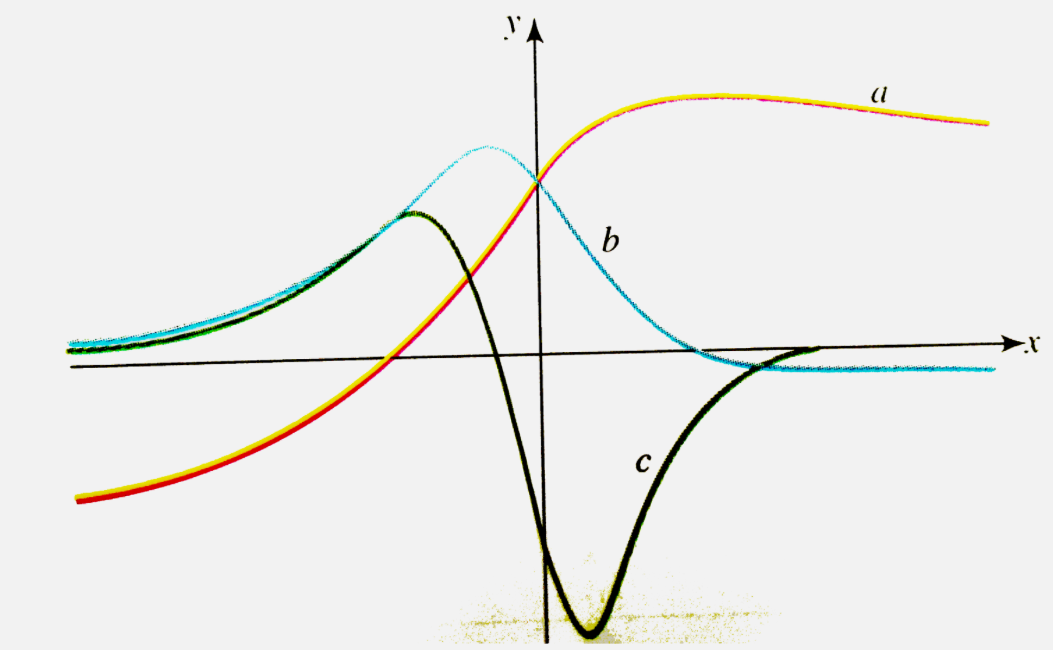
The figure shows the graphs of f, f' and f''. Indentify each curve and explain your choices.
 Solution in Bengali
Solution in Bengali
Clearly the graph 'a' and 'b' are lying entirely above the x-axis. Now for graph 'b', derivative becomes zero at point p.

For graph 'c', derivative becomes zero at x = q and x = r.
Now none of the graphs meets the x-axis at two points q and r.
Hence 'a' must be the graph of the derivative of graph 'b'. Also for x = p, the graph of 'a' meets the x-axis , which confirms this fact.
Let 'b' be the graph of y = f(x) and 'a' be the graph of y = f'(x) , then can 'c' be the graph of y = f''(x)?
Certainly not, as otherwise graph 'c' had cut the x-axis twice.
So 'c' is the graph of y=f(x). 'b' is the graph of y = f'(x) and 'a' is the graph of y = f''(x).
Also for graph 'c', the angle of tangent with + ve x -axis is acute and increases till the point x = p. After x = p and onwards, angle decreases but remains positive. Thus, the graph of y = f'(x) , which is graph is graph 'b' , line entirely above the x-axis. In other words. the graph of 'c' is entirely increasing, hence its derivative is positive, as a result graph 'b', which is the graph of y = f'(x), lies above x - axis.
So finally c is y = f(x), b is y = f'(x) and a = f'(x).
Topper's Solved these Questions
- GETTING STARTED WITH GRAPHSBOOK - CENGAGE PUBLICATIONCHAPTER - GETTING STARTED WITH GRAPHSEXERCISE - ILLUSTRATION 1.26
1 Videos
- GETTING STARTED WITH GRAPHSBOOK - CENGAGE PUBLICATIONCHAPTER - GETTING STARTED WITH GRAPHSEXERCISE - ILLUSTRATION 1.27
1 Videos
- GETTING STARTED WITH GRAPHSBOOK - CENGAGE PUBLICATIONCHAPTER - GETTING STARTED WITH GRAPHSEXERCISE - ILLUSTRATION 1.24
1 Videos
- FUNCTIONSBOOK - CENGAGE PUBLICATIONCHAPTER - FUNCTIONSEXERCISE - Comprehension Type
7 Videos
- GRAPH OF INVERSE TRIGONOMETRIC FUNCTIONSBOOK - CENGAGE PUBLICATIONCHAPTER - GRAPH OF INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Exercises
18 Videos
Similar Questions
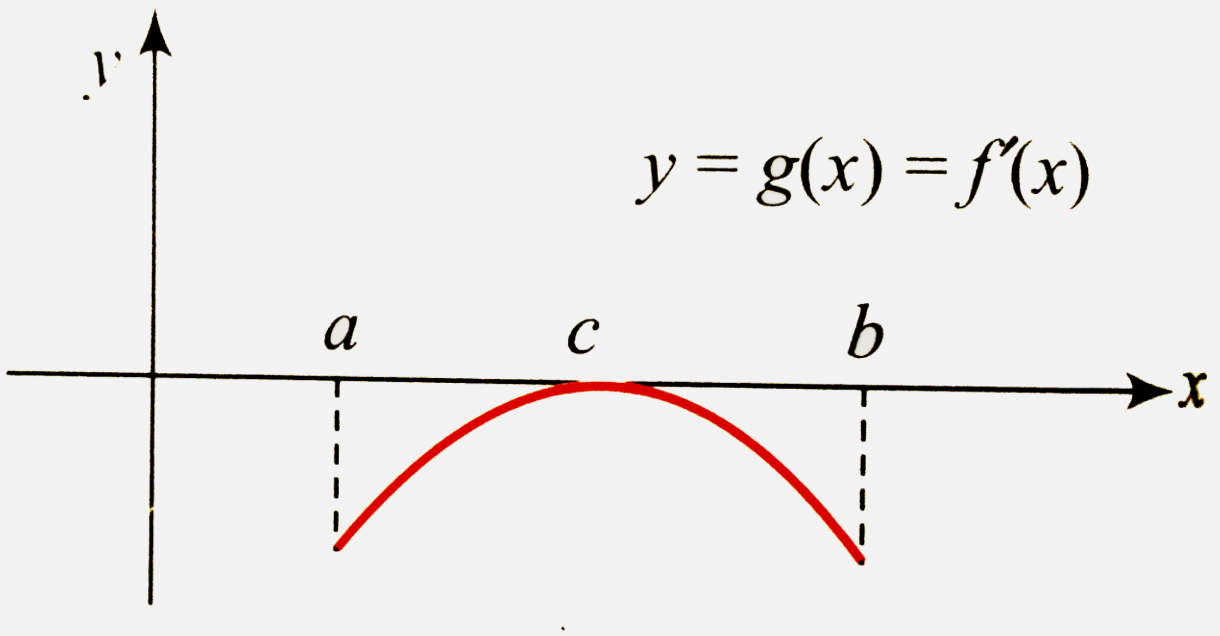
Following is the graph of y = f' (x) , given that f(c) = 0. Analyse the graph and answer the following questions.
(a) How many times the graph of y = f(x) will intersect the x - axis?
(b) Discuss the type of roots of the equation f (x) = 0, a≤x≤b.
(c) How many points of inflection the graph of y=f(x),a≤x≤b, has?
,(d) Find the points of local maxima/minima of y=f(x),a≤x≤b,
, (e) f"(x)=0 has how many roots?
View SolutionFind the asymptote of the function y=2x2+3x+1x if any.
View Solution
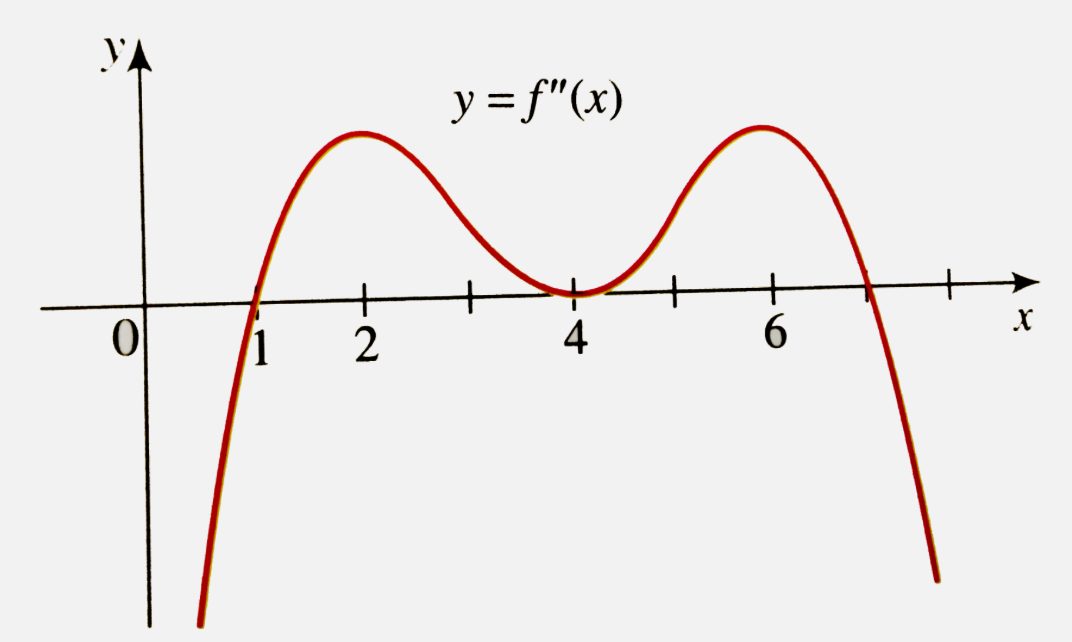
The graph of the second derivation f''(x) is given in the following figure. State the x - coordinate of the point of inflection of f. Given reasons for your answer.
View SolutionLet f(x)=x2−2x−1∀x∈R.Letf:(−∞,a]→[b,∞), where a is the largest real number for which f(x) is bijective.
If f:R→R, then range of values of k for which equation f(|x|)=k has 4 distinct real roots is
View SolutionDraw the graph of y=tan−1x−cot−1x.
View SolutionThe figure shows the graphs of f, f' and f'' . Identify each curve and explain your choices.
(##CEN_GRA_C01_S01_025_Q01.png" width="80%">
View SolutionThe figure shows the graphs of f, f' and f''. Indentify each curve and explain your choices.

View SolutionHow many lines of symmetry does the above figure have ?
View SolutionDetermine the point of symmetry of a regular hexagon.
View SolutionDtermine the images of the following figure about the given line :
View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionMatch the following Column A to Column B

View SolutionFind the area of the figure given below.
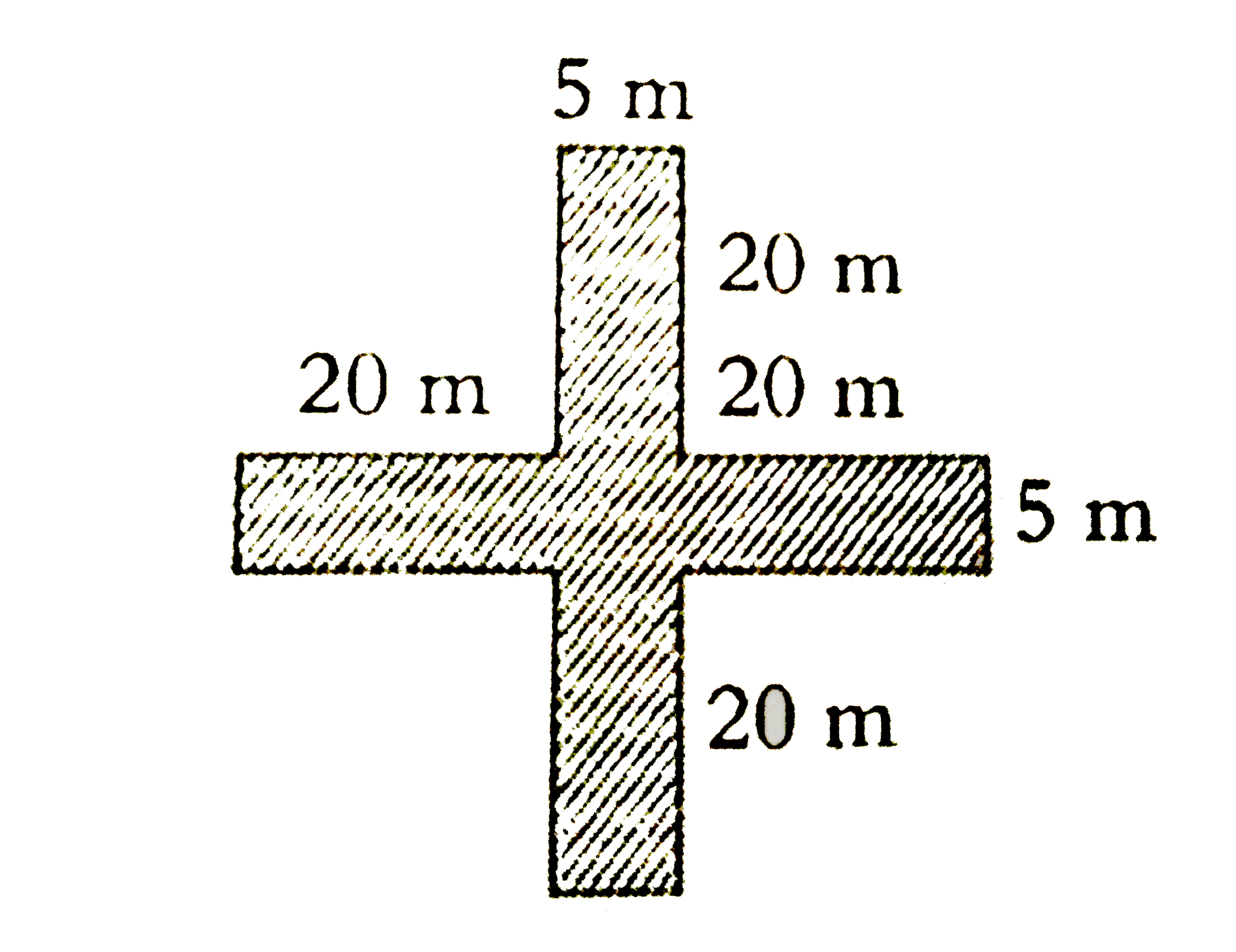
View SolutionThe area of the shaded part in the figure given below is ______.
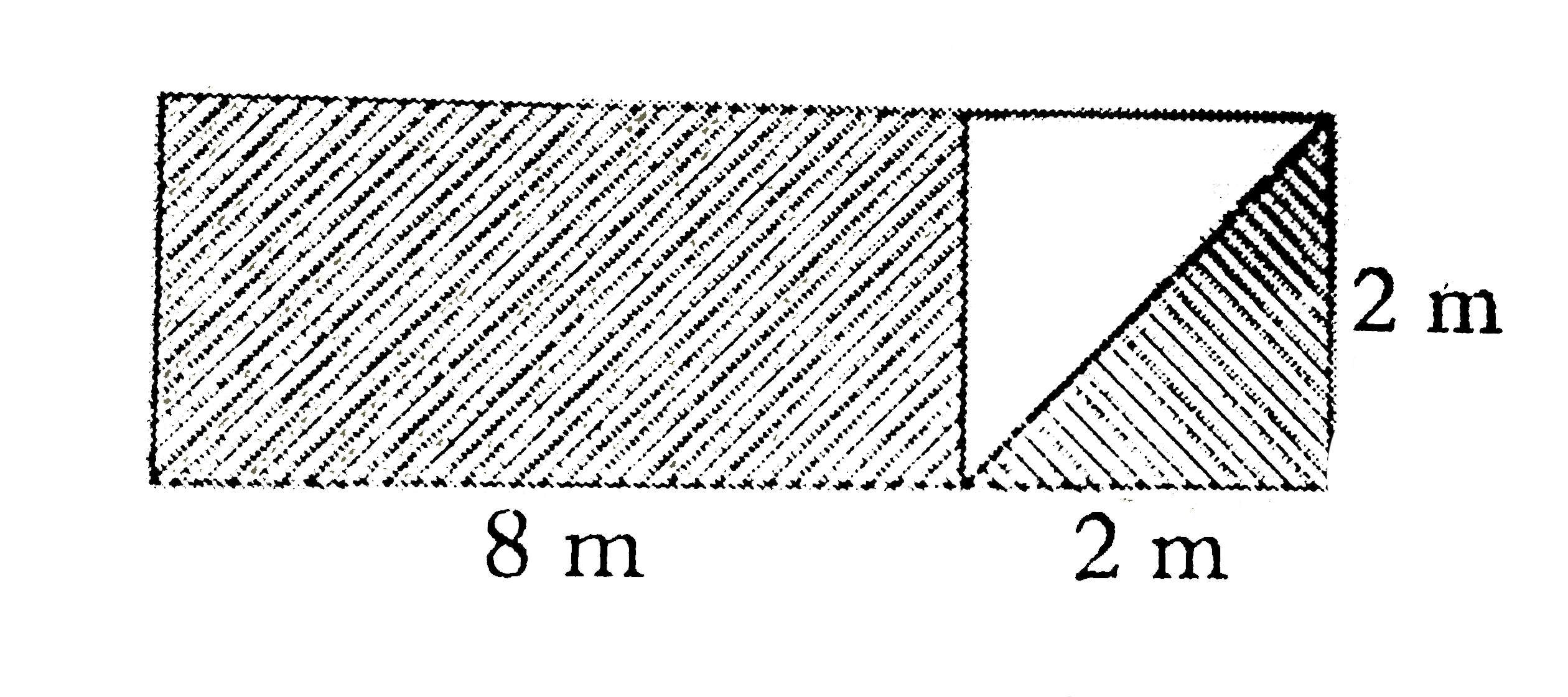
View SolutionThe inequation represented by the graph given below is :
View Solution
