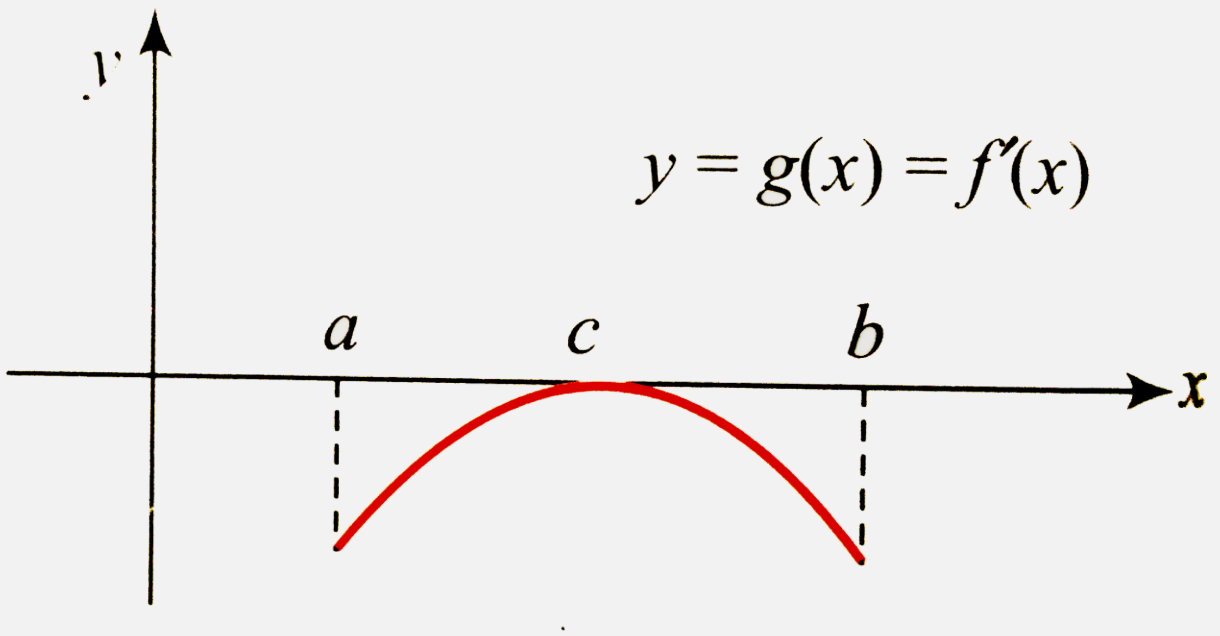
Following is the graph of y = f' (x) , given that f(c) = 0. Analyse the graph and answer the following questions.
(a) How many times the graph of y = f(x) will intersect the x - axis?
(b) Discuss the type of roots of the equation f (x) = 0, a≤x≤b.
(c) How many points of inflection the graph of y=f(x),a≤x≤b, has?
,(d) Find the points of local maxima/minima of y=f(x),a≤x≤b,
,
(e) f"(x)=0 has how many roots?
 Solution in Bengali
Solution in Bengali
(a) f'(x)≤0,∀x∈[a,b], so f(x) is a decreasing function and f(c)=0⇒f(x) is a decreasing function and x(c)=0⇒f(x) cuts x - axis once when x = c.
(b) We note that f(c) = 0, f'(c) = 0. Also tangent to f'(x) at x = c is y = 0. So f''(c) = 0 Therefore, x = c is repeated root of third order. So the equation f(x) = 0 has at least three repeated roots.
(c) We have f''(c) = 0 . So the graph of y = f (x) has one point of inflection at x = c.
(d) As f (x) is a decreasing function for all x∈(a,b),f(x) has no local maxima or minima.
(e) f''(c)=0⇒c is a root of f''(x) = 0.
Topper's Solved these Questions
- BOOK - CENGAGE PUBLICATIONCHAPTER - GETTING STARTED WITH GRAPHSEXERCISE - ILLUSTRATION 1.271videos
GETTING STARTED WITH GRAPHS
- BOOK - CENGAGE PUBLICATIONCHAPTER - GETTING STARTED WITH GRAPHSEXERCISE - ILLUSTRATION 1.281videos
GETTING STARTED WITH GRAPHS
- BOOK - CENGAGE PUBLICATIONCHAPTER - GETTING STARTED WITH GRAPHSEXERCISE - ILLUSTRATION 1.251videos
GETTING STARTED WITH GRAPHS
- BOOK - CENGAGE PUBLICATIONCHAPTER - FUNCTIONSEXERCISE - Comprehension Type7videos
FUNCTIONS
- BOOK - CENGAGE PUBLICATIONCHAPTER - GRAPH OF INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Exercises18videos
GRAPH OF INVERSE TRIGONOMETRIC FUNCTIONS
Similar Questions
Find the asymptote of the function y=2x2+3x+1x if any.
View SolutionFind the horizontal, vertical and oblique asymptotes of each of the curves.
(a)y=xx+4(b)y=x2+4x2−1(c)y=x3x2+3x−10(d)y=x3+1x3+x(e)y=x4√x4+1(f)y=x−9√4x2+3x+2(g)y=12x−1(h)y=1logex(i)y=12x+1View SolutionThe figure shows the graphs of f, f' and f''. Indentify each curve and explain your choices.
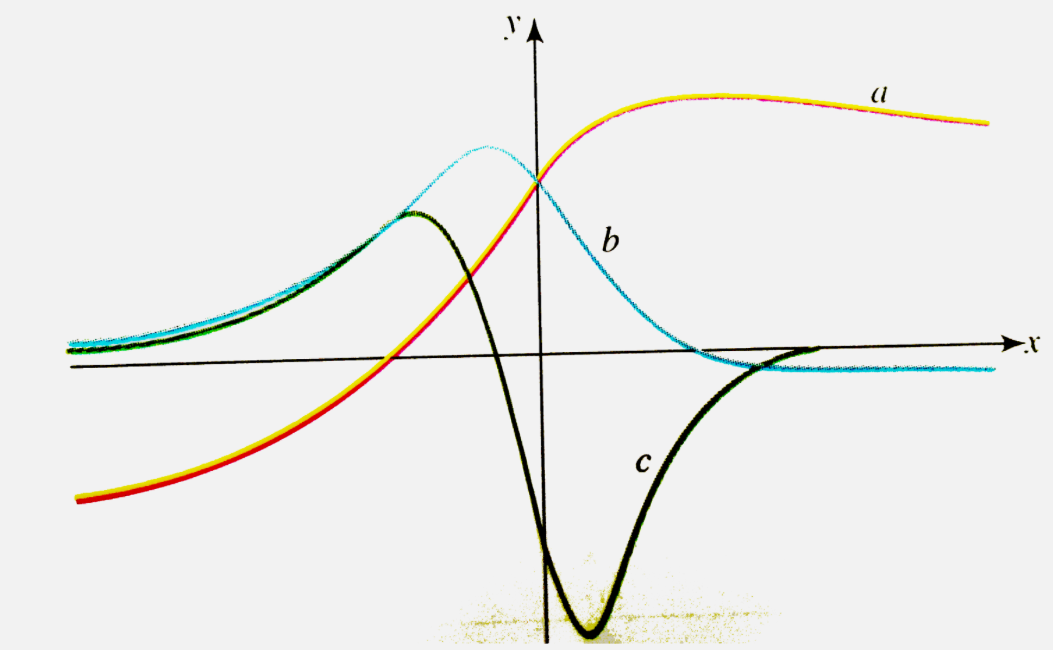 View Solution
View SolutionLet f(x)=x2−2x−1∀x∈R.Letf:(−∞,a]→[b,∞), where a is the largest real number for which f(x) is bijective.
If f:R→R, then range of values of k for which equation f(|x|)=k has 4 distinct real roots is05:00View SolutionDraw the graph of y=tan−1x−cot−1x.
03:45View SolutionThe diagram shows the graph of the derivative of a functin f(x) for 0≤x≤4 with f(0) = 0. Which of the following could be correct statements for y = f(x)?
(##CENGRAC01S01021_Q01.png width=80%><br>(a)Tan≥ntl∈e→y=f(x)atx=0makesan∠of sec^(-1) sqrt 5 with the x - axis.
(b) f is increasing in (0, 3).
(c) x = 1 is both an inflection point and the point of local extremum.
(d) Number of critical point on y = f(x) is two.05:30View SolutionFollowing is the graph of y = f' (x) , given that f(c) = 0. Analyse the graph and answer the following questions.
(a) How many times the graph of y = f(x) will intersect the x - axis?
(b) Discuss the type of roots of the equation f (x) = 0, a≤x≤b.
(c) How many points of inflection the graph of y=f(x),a≤x≤b, has?
(d) Find the points of local maxima/minima ofy=f(x),a<xb.
(e) How many roots equation f''(x)=0 has?
 04:55View Solution
04:55View SolutionThe graph of y = f(x) is given with six labelled points. Anser the following questions.
(a) At which point f'(x) has the greatest value?
(b) At which point f(x) and f'(x) both are zero?
(c) At how many point f'(x) is negative ?
(d) Which is the point of infection?
 03:57View Solution
03:57View SolutionThe graph of y=f(x) is given below
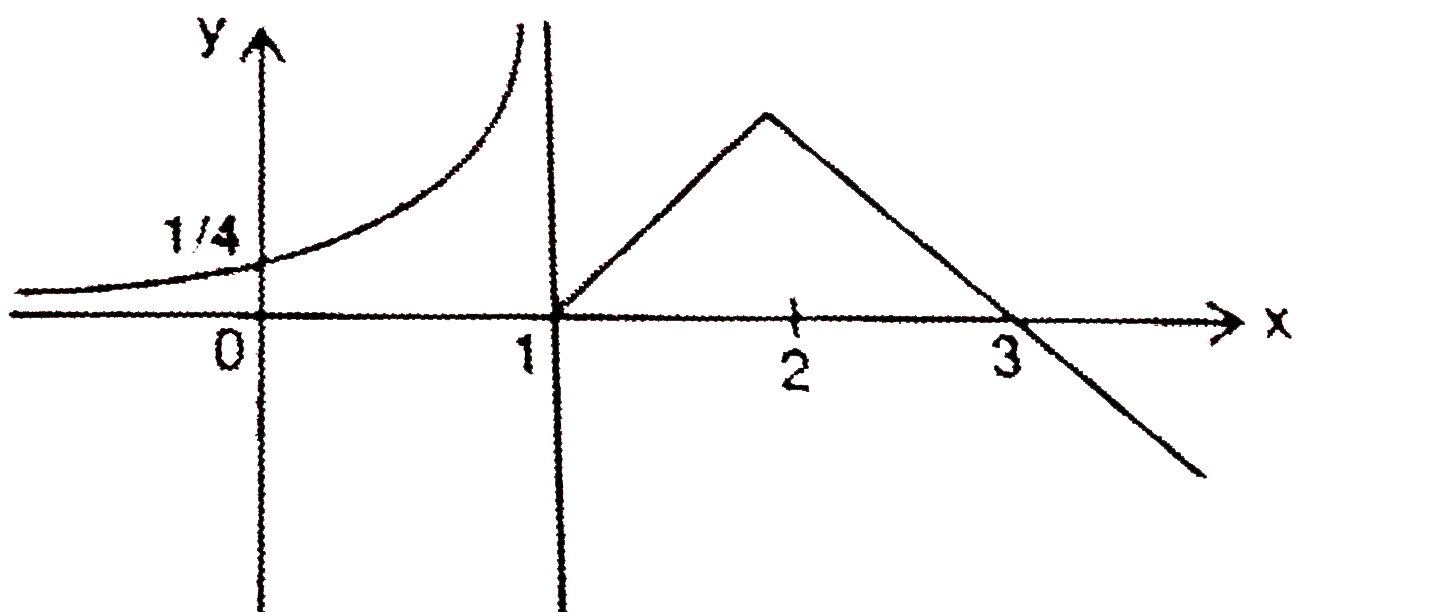
then the graph y=|f(|x|)| is :01:00View SolutionFollowing is the graph of y = f(x).
<imga≤ocr_imageload∈g=lazysrc=https://d10lpgp6xz60nq.cloudfront.net/physics_images/CEN_GRA_C01_S01_005_Q01.pngwh=80%mx-autosty≤=background:white;><br>F∈dthes√oftheequation f(x) = 0, f(x) = 4 and f(x) = 10.02:23View SolutionThe diagram shows the graph of the derivative of a functin f(x) for 0≤x≤4 with f(0) = 0. Which of the following could be correct statements for y = f(x)?
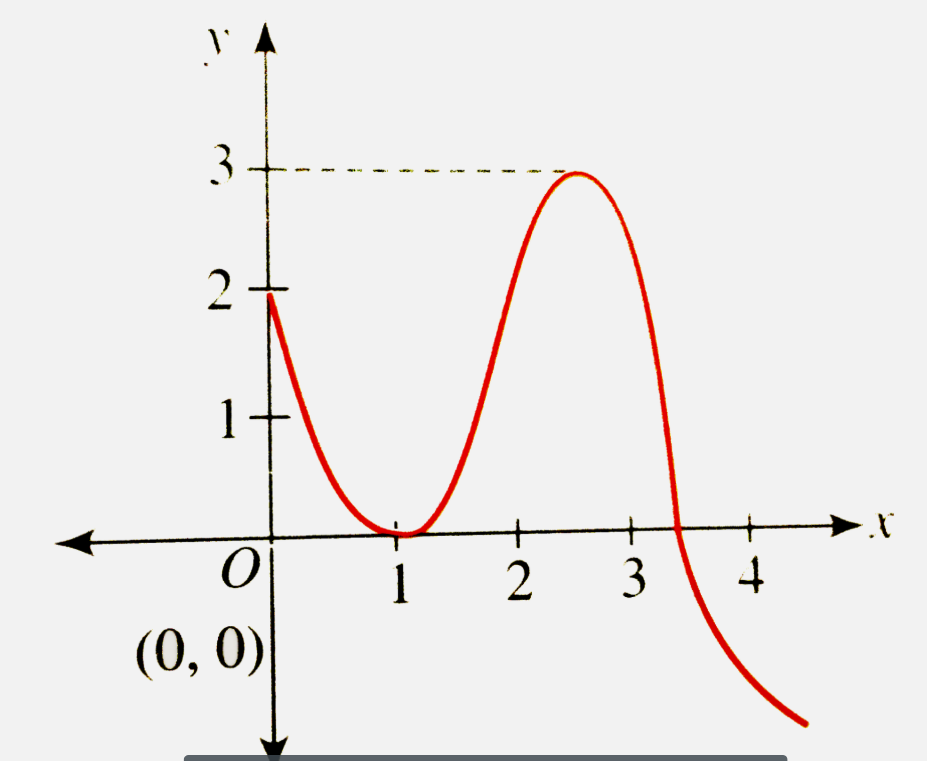
(a) Tangent line to y = f(x) at x = 0 makes an angle of sec−1√5 with the x - axis.
(b) f is increasing in (0, 3).
(c) x = 1 is both an inflection point and the point of local extremum.
(d) Number of critical point on y = f(x) is two.06:16View SolutionFollowing is the graph of y = f' (x) , given that f(c) = 0. Analyse the graph and answer the following questions.
(a) How many times the graph of y = f(x) will intersect the x - axis?
(b) Discuss the type of roots of the equation f (x) = 0, a≤x≤b.
(c) How many points of inflection the graph of y=f(x),a≤x≤b, has?
(d) Find the points of local maxima/minima ofy=f(x),a<xb.
(e) How many roots equation f''(x)=0 has?
 05:11View Solution
05:11View SolutionThe graph of y = f(x) is given with six labelled points. Anser the following questions.
(a) At which point f'(x) has the greatest value?
(b) At which point f(x) and f'(x) both are zero?
(c) At how many point f'(x) is negative ?
(d) Which is the point of infection?
 04:05View Solution
04:05View SolutionThe graph of y =g(x) =f(X) is as shown in the following figure analyse this graph and answer the following question

Number of points of inflectionn the graph of y = f(x) for a<x<b has04:56View SolutionThe graph of y=f(x) is given below

then the graph y=|f(|x|)| is :07:38View Solution

