The following table gives the number of finished articles turned out per day be different number of workers in a factors. Find the standard deviation of the daily output of finished articles. Find the variance and standard deviation of the following frequency distribution: Number of article:, 18, 19, 20, 21, 22, 23, 24, 25, 26, 27 No. of workers:, 3, 7, 11, 14, 18, 17, 13, 8, 5, 4
To find the variance and standard deviation of the given frequency distribution, we will follow these steps:
Step 1: Create a Frequency Distribution Table
We have the following data:
| Number of Articles (Xi) | Number of Workers (fi) |
|-------------------------|------------------------|
| 18 | 3 |
| 19 | 7 |
| 20 | 11 |
| 21 | 14 |
| 22 | 18 |
| 23 | 17 |
| 24 | 13 |
| 25 | 8 |
| 26 | 5 |
| 27 | 4 |
Step 2: Calculate the Assumed Mean (a)
Let's assume the mean (a) to be 22.
Step 3: Calculate di (Deviation from Mean)
Calculate di=Xi−a:
| Xi | di |
|-----|-----|
| 18 | -4 |
| 19 | -3 |
| 20 | -2 |
| 21 | -1 |
| 22 | 0 |
| 23 | 1 |
| 24 | 2 |
| 25 | 3 |
| 26 | 4 |
| 27 | 5 |
Step 4: Calculate fi * di
Now calculate fi⋅di:
| Xi | fi | di | fi * di |
|-----|----|-----|---------|
| 18 | 3 | -4 | -12 |
| 19 | 7 | -3 | -21 |
| 20 | 11 | -2 | -22 |
| 21 | 14 | -1 | -14 |
| 22 | 18 | 0 | 0 |
| 23 | 17 | 1 | 17 |
| 24 | 13 | 2 | 26 |
| 25 | 8 | 3 | 24 |
| 26 | 5 | 4 | 20 |
| 27 | 4 | 5 | 20 |
Step 5: Calculate di²
Calculate di2:
| Xi | di | di² |
|-----|-----|-----|
| 18 | -4 | 16 |
| 19 | -3 | 9 |
| 20 | -2 | 4 |
| 21 | -1 | 1 |
| 22 | 0 | 0 |
| 23 | 1 | 1 |
| 24 | 2 | 4 |
| 25 | 3 | 9 |
| 26 | 4 | 16 |
| 27 | 5 | 25 |
Step 6: Calculate fi * di²
Now calculate fi⋅di2:
| Xi | fi | di² | fi * di² |
|-----|----|-----|----------|
| 18 | 3 | 16 | 48 |
| 19 | 7 | 9 | 63 |
| 20 | 11 | 4 | 44 |
| 21 | 14 | 1 | 14 |
| 22 | 18 | 0 | 0 |
| 23 | 17 | 1 | 17 |
| 24 | 13 | 4 | 52 |
| 25 | 8 | 9 | 72 |
| 26 | 5 | 16 | 80 |
| 27 | 4 | 25 | 100 |
Step 7: Calculate Σfi, Σfi * di, and Σfi * di²
- Σfi=3+7+11+14+18+17+13+8+5+4=100
- Σfi⋅di=−12−21−22−14+0+17+26+24+20+20=38
- Σfi⋅di2=48+63+44+14+0+17+52+72+80+100=490
Step 8: Calculate Variance (σ²)
Using the formula for variance:
σ2=Σfi⋅di2Σfi−(Σfi⋅diΣfi)2
Substituting the values:
σ2=490100−(38100)2
σ2=4.9−0.1444=4.7556≈4.76
Step 9: Calculate Standard Deviation (σ)
Standard deviation is the square root of variance:
σ=√σ2=√4.76≈2.18
Final Answers
- Variance (σ²) ≈ 4.76
- Standard Deviation (σ) ≈ 2.18
We have the following data:
|-------------------------|------------------------|
| 18 | 3 |
| 19 | 7 |
| 20 | 11 |
| 21 | 14 |
| 22 | 18 |
| 23 | 17 |
| 24 | 13 |
| 25 | 8 |
| 26 | 5 |
| 27 | 4 |
Let's assume the mean (a) to be 22.
Calculate di=Xi−a:
|-----|-----|
| 18 | -4 |
| 19 | -3 |
| 20 | -2 |
| 21 | -1 |
| 22 | 0 |
| 23 | 1 |
| 24 | 2 |
| 25 | 3 |
| 26 | 4 |
| 27 | 5 |
Now calculate fi⋅di:
|-----|----|-----|---------|
| 18 | 3 | -4 | -12 |
| 19 | 7 | -3 | -21 |
| 20 | 11 | -2 | -22 |
| 21 | 14 | -1 | -14 |
| 22 | 18 | 0 | 0 |
| 23 | 17 | 1 | 17 |
| 24 | 13 | 2 | 26 |
| 25 | 8 | 3 | 24 |
| 26 | 5 | 4 | 20 |
| 27 | 4 | 5 | 20 |
Calculate di2:
|-----|-----|-----|
| 18 | -4 | 16 |
| 19 | -3 | 9 |
| 20 | -2 | 4 |
| 21 | -1 | 1 |
| 22 | 0 | 0 |
| 23 | 1 | 1 |
| 24 | 2 | 4 |
| 25 | 3 | 9 |
| 26 | 4 | 16 |
| 27 | 5 | 25 |
Now calculate fi⋅di2:
|-----|----|-----|----------|
| 18 | 3 | 16 | 48 |
| 19 | 7 | 9 | 63 |
| 20 | 11 | 4 | 44 |
| 21 | 14 | 1 | 14 |
| 22 | 18 | 0 | 0 |
| 23 | 17 | 1 | 17 |
| 24 | 13 | 4 | 52 |
| 25 | 8 | 9 | 72 |
| 26 | 5 | 16 | 80 |
| 27 | 4 | 25 | 100 |
- Σfi=3+7+11+14+18+17+13+8+5+4=100
- Σfi⋅di=−12−21−22−14+0+17+26+24+20+20=38
- Σfi⋅di2=48+63+44+14+0+17+52+72+80+100=490
Using the formula for variance:
σ2=Σfi⋅di2Σfi−(Σfi⋅diΣfi)2
Substituting the values:
σ2=490100−(38100)2
σ2=4.9−0.1444=4.7556≈4.76
Standard deviation is the square root of variance:
σ=√σ2=√4.76≈2.18
- Variance (σ²) ≈ 4.76
- Standard Deviation (σ) ≈ 2.18
Topper's Solved these Questions
Similar Questions
Find the variance and standard deviation of the following data:
 View Solution
View SolutionFind the mean and standard deviation of the following frequency distribution :
 View Solution
View SolutionFind the variance and standard deviation from the following data:
 View Solution
View SolutionFind the variance and standard deviation of the following distribution
 View Solution
View SolutionEstimate standard deviation for the following frequency distribution.
 View Solution
View SolutionFind the variance and standard deviation for the following distribution.
 View Solution
View SolutionCalculate variance and standard deviation for the following distribution.
 View Solution
View SolutionFind the standard deviation of the following distribution :
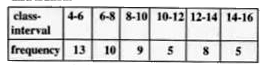 View Solution
View SolutionFind the variance and standard deviation of the following data 5,12,3,18,6,8,2,10
View SolutionFind out the standard deviation from the following distribution table:
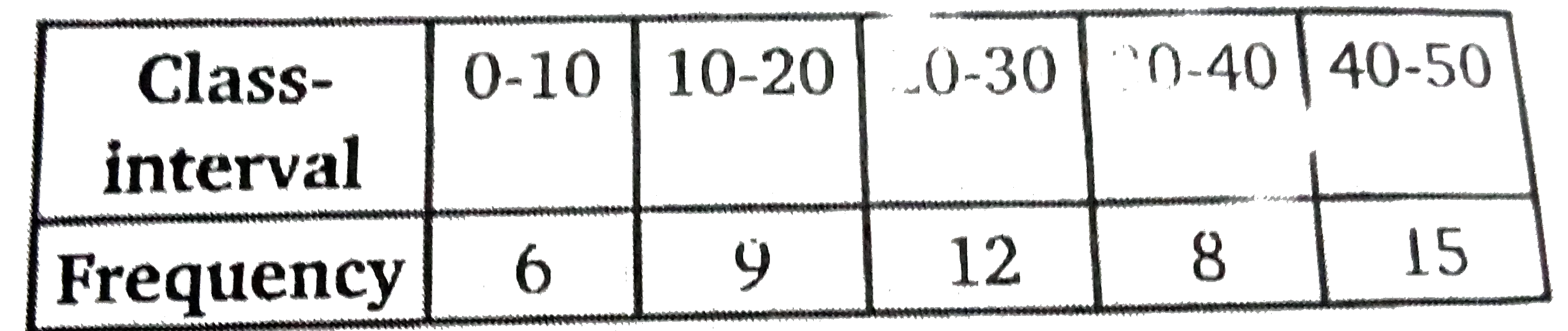 View Solution
View Solution

