The given figure shows the cross-section of a cone, a cylinder and a hemisphere all with the same diameter 10 cm, and the other dimensions are as shown. Calculate the total surface area.
The correct Answer is:738.57cm2
To find the total surface area of the given figure consisting of a cone, cylinder, and hemisphere, all with the same diameter of 10 cm, we will follow these steps:
1. Find the Radius:
- Given the diameter of the figures is 10 cm, the radius r can be calculated as:
r=diameter2=10 cm2=5 cm
2. Identify the Heights:
- The height of the cone hc is given as 12 cm.
- The height of the cylinder hcy is also given as 12 cm.
3. Calculate the Slant Height of the Cone:
- The slant height l of the cone can be calculated using the Pythagorean theorem:
l=√h2c+r2=√122+52=√144+25=√169=13 cm
4. Calculate the Surface Areas:
- Surface Area of the Cone:
Surface Area of Cone=πrl+πr2=π(5)(13)+π(52)=65π+25π=90π
- Surface Area of the Cylinder:
Surface Area of Cylinder=2πrhcy+2πr2=2π(5)(12)+2π(52)=120π+50π=170π
- Surface Area of the Hemisphere:
Surface Area of Hemisphere=2πr2=2π(52)=50π
5. Total Surface Area Calculation:
- Now, we can sum the surface areas of the cone, cylinder, and hemisphere:
Total Surface Area=Surface Area of Cone+Surface Area of Cylinder+Surface Area of Hemisphere
Total Surface Area=90π+170π+50π=310π
6. Substituting the Value of π:
- Using π≈227:
Total Surface Area=310×227=68207≈974.29 cm2
Final Answer:
The total surface area of the given figure is approximately 974.29 cm2.
- Given the diameter of the figures is 10 cm, the radius r can be calculated as:
r=diameter2=10 cm2=5 cm
- The height of the cone hc is given as 12 cm.
- The height of the cylinder hcy is also given as 12 cm.
- The slant height l of the cone can be calculated using the Pythagorean theorem:
l=√h2c+r2=√122+52=√144+25=√169=13 cm
- Surface Area of the Cone:
Surface Area of Cone=πrl+πr2=π(5)(13)+π(52)=65π+25π=90π
- Surface Area of the Cylinder:
Surface Area of Cylinder=2πrhcy+2πr2=2π(5)(12)+2π(52)=120π+50π=170π
- Surface Area of the Hemisphere:
Surface Area of Hemisphere=2πr2=2π(52)=50π
- Now, we can sum the surface areas of the cone, cylinder, and hemisphere:
Total Surface Area=Surface Area of Cone+Surface Area of Cylinder+Surface Area of Hemisphere
Total Surface Area=90π+170π+50π=310π
- Using π≈227:
Total Surface Area=310×227=68207≈974.29 cm2
The total surface area of the given figure is approximately 974.29 cm2.
Topper's Solved these Questions
Similar Questions
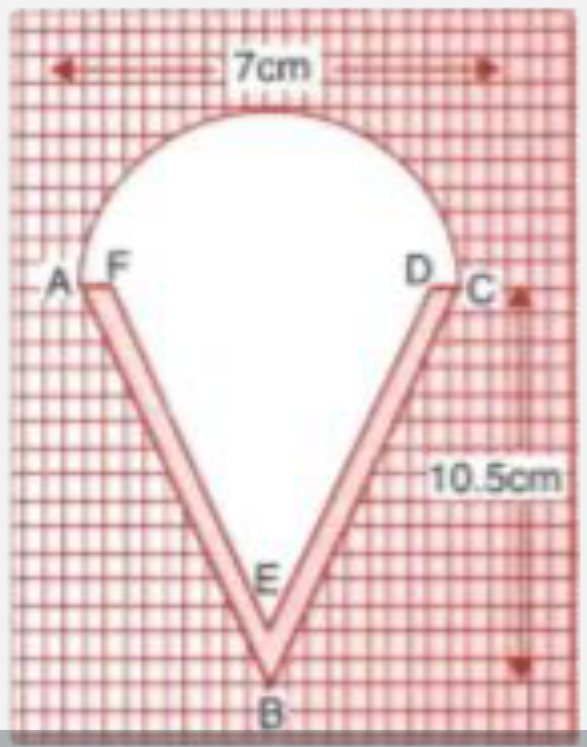
The given figure shows the cross-section of an ice cream cone consisting of a cone surmounted by a hemisphere. The radius of the hemisphere is 3.5 cm and the height of the cone is 10-5 cm. The outer shell ABCDEF is shaded and is not filled with ice-cream. AF = DC = 0.5 cm, AB // FE and BC // ED. Calculate :
(i) the volume of the ice-cream in the cone (the internal volume of the cone including the hemisphere) in cm3,
(ii) the volume of the outer shell (the shaded portion) in cm3.
In each case, give your answer correct to the nearest cm3.
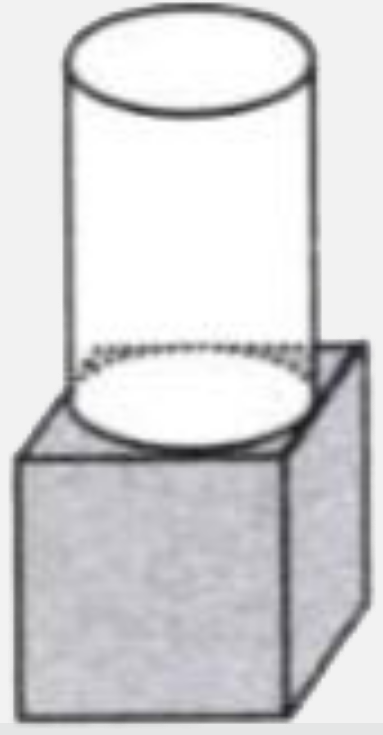
View SolutionA cubical block of side 7 cm is surmounted by a hemisphere. What is the greatest diameter of the hemisphere can have? Find the total surface area of the solid.
View SolutionA right cylinder , a right cone and a hemishpere have the same heightr and sthe same base area .Find the ratio of their (i) volumes (ii) total surface areas.
View SolutionA metal container in the form of a cylinder is surmounted by a hemisphere of the same radius. The internal height of the cylinder is 7 m and the internal radius is 3-5 m. Calculate :
the total area of the internal surface, excluding the base,
View SolutionA toy is in the form of a cone mounted on a hemisphere of same radius 7 cm. If the total height of the toy is 31cm, find the total surface area.
View SolutionA decorative block shown in Figure is made of two solids a cube and a hemisphere. The base of the block is a cube with edge 5 cm, and the hemisphere fixed on the top has a diameter 4.2 cm. Find the total surface area of the block (Take π=22/7 ).
View SolutionA toy is in the form of a cone mounted on a hemisphere with the same radius. The diameter of the base of the conical portion is 6 cm and its height is 4 cm. Determine the surface area of the toy (Use π=3.14 )
View SolutionA toy is in the form of a cone mounted on a hemisphere with the same radius. The diameter of the base of the conical portion is 12 cm and its height is 8 cm. Determine the surface area and the volume of the toy (π=3.14).
View SolutionThe given figure shows a solid formed of a solid cube of side 40 cm and a solid cylinder of radius 20 cm and height 50 cm attached to the cube as shown. Find the volume and the total surface area of the whole solid [Take π=3.14]
View SolutionA rocket is in the form of a circular cylinder closed at the lower end with a cone of the same radius attached to the top. The cylinder is of radius 2.5 m and height 21 m and the cone has the slant height 8 m. Calculate the total surface area and the volume of the rocket.
View Solution
