The graph of the function y=f(x) is shown.
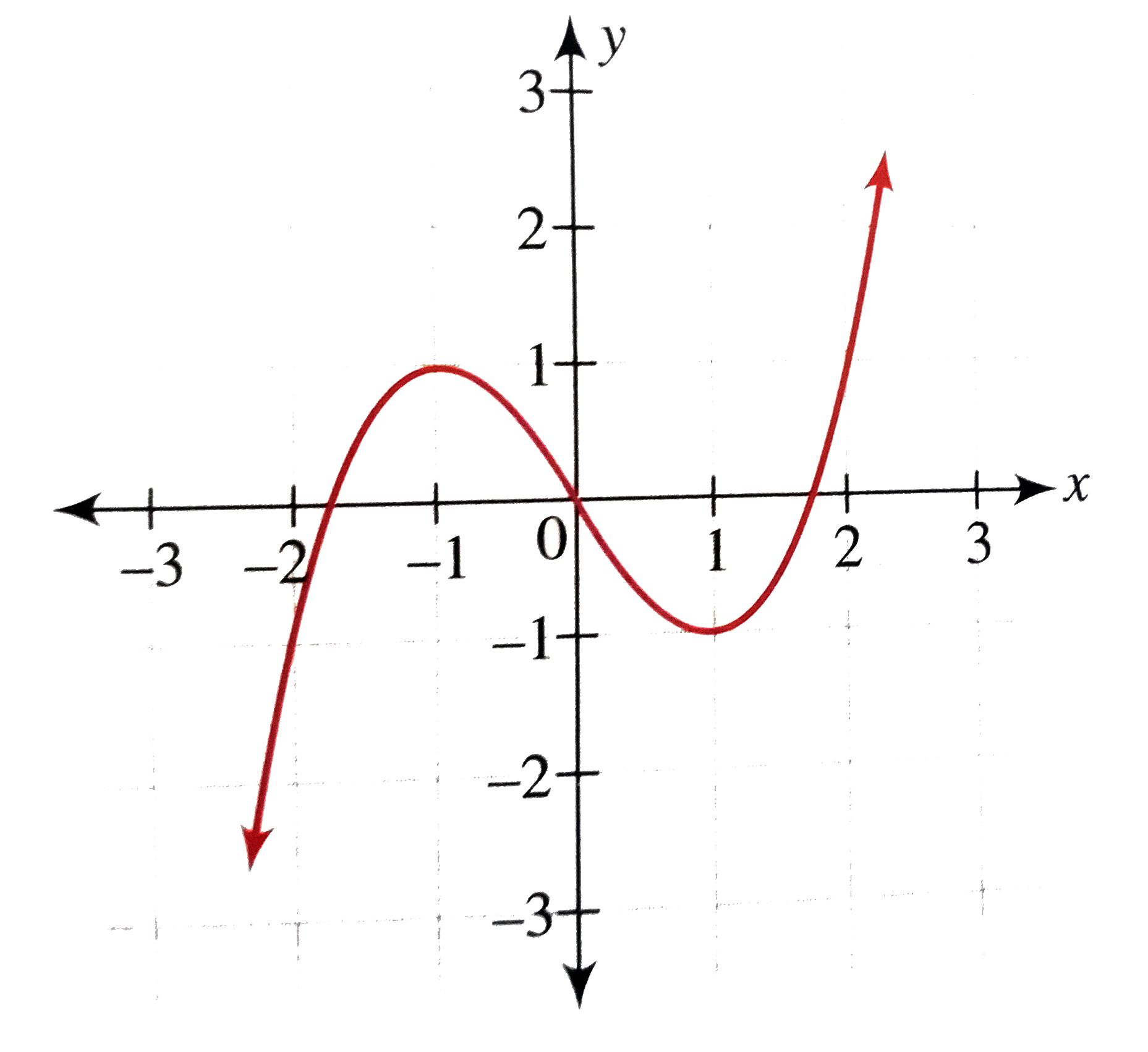
Find the number of solutions to the equation ||f(x)|−1|=12.
Video Solution
Text Solution
We have ||f(x)|−1|=12
From the given graph, first obtain the graph of ||f(x)|−1| in the following steps.
Step 1:
Graph of y=|f(x)|
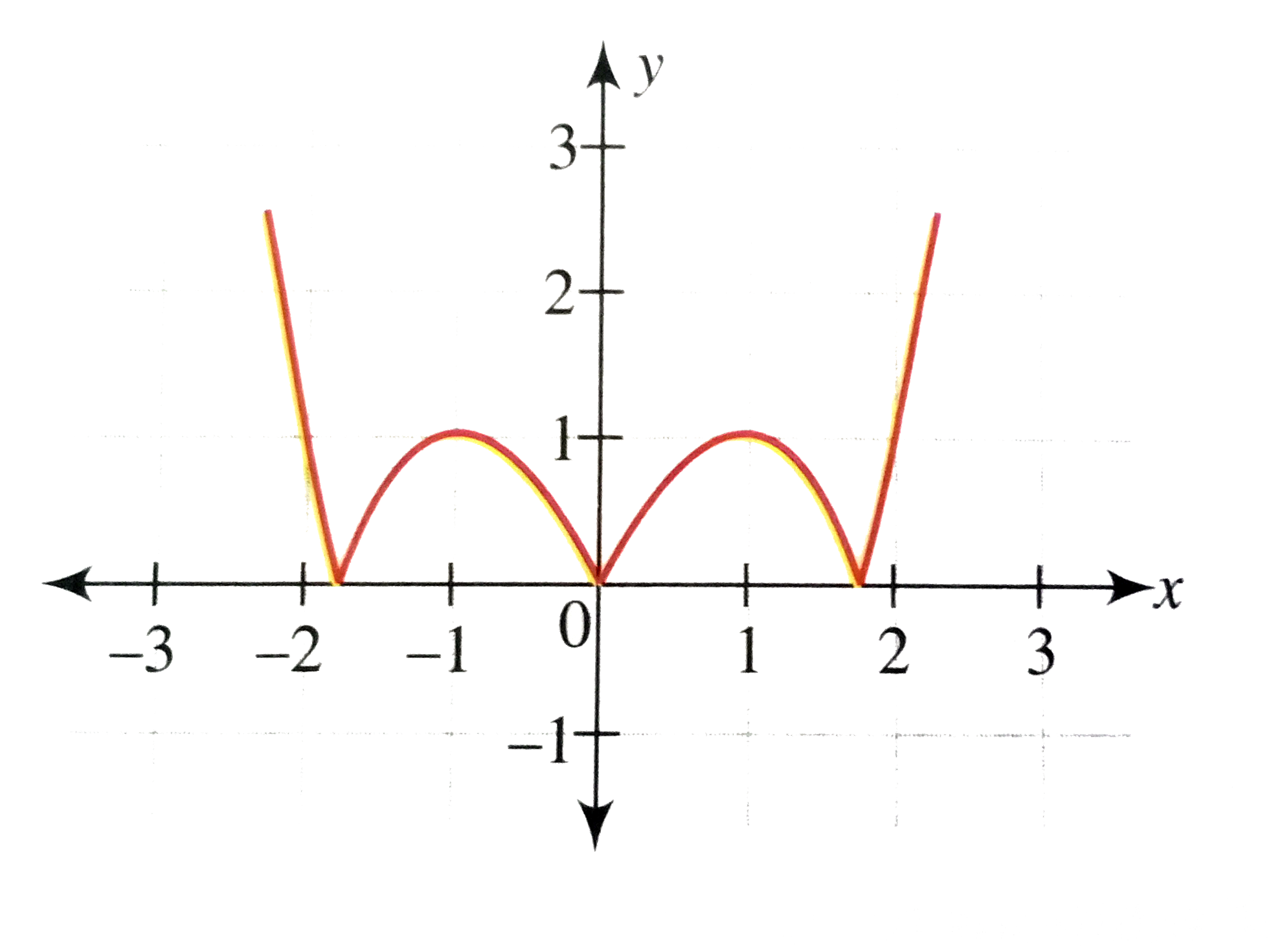
Step 2 :
Graph of y=|f(x)|−1
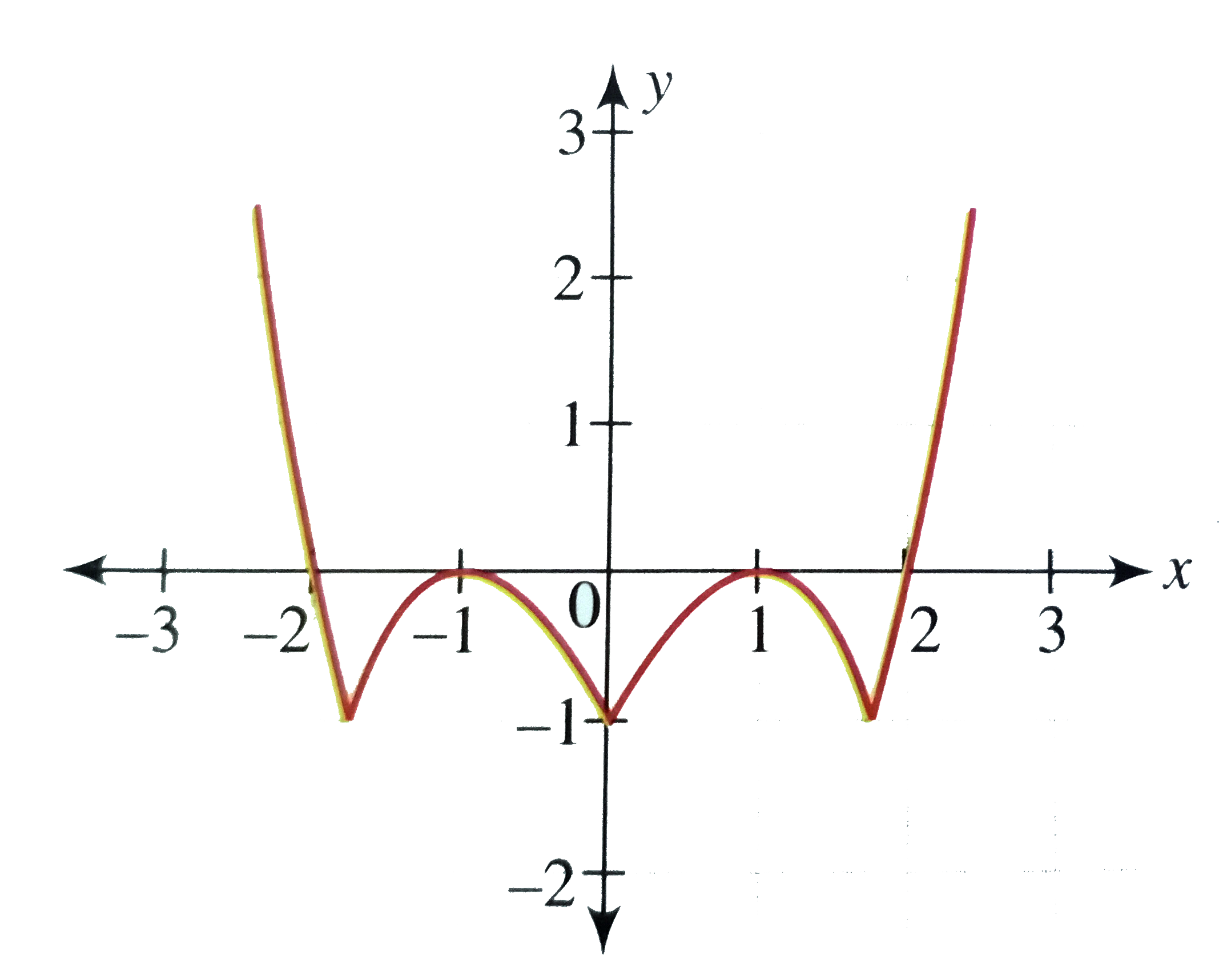
Step 3 :
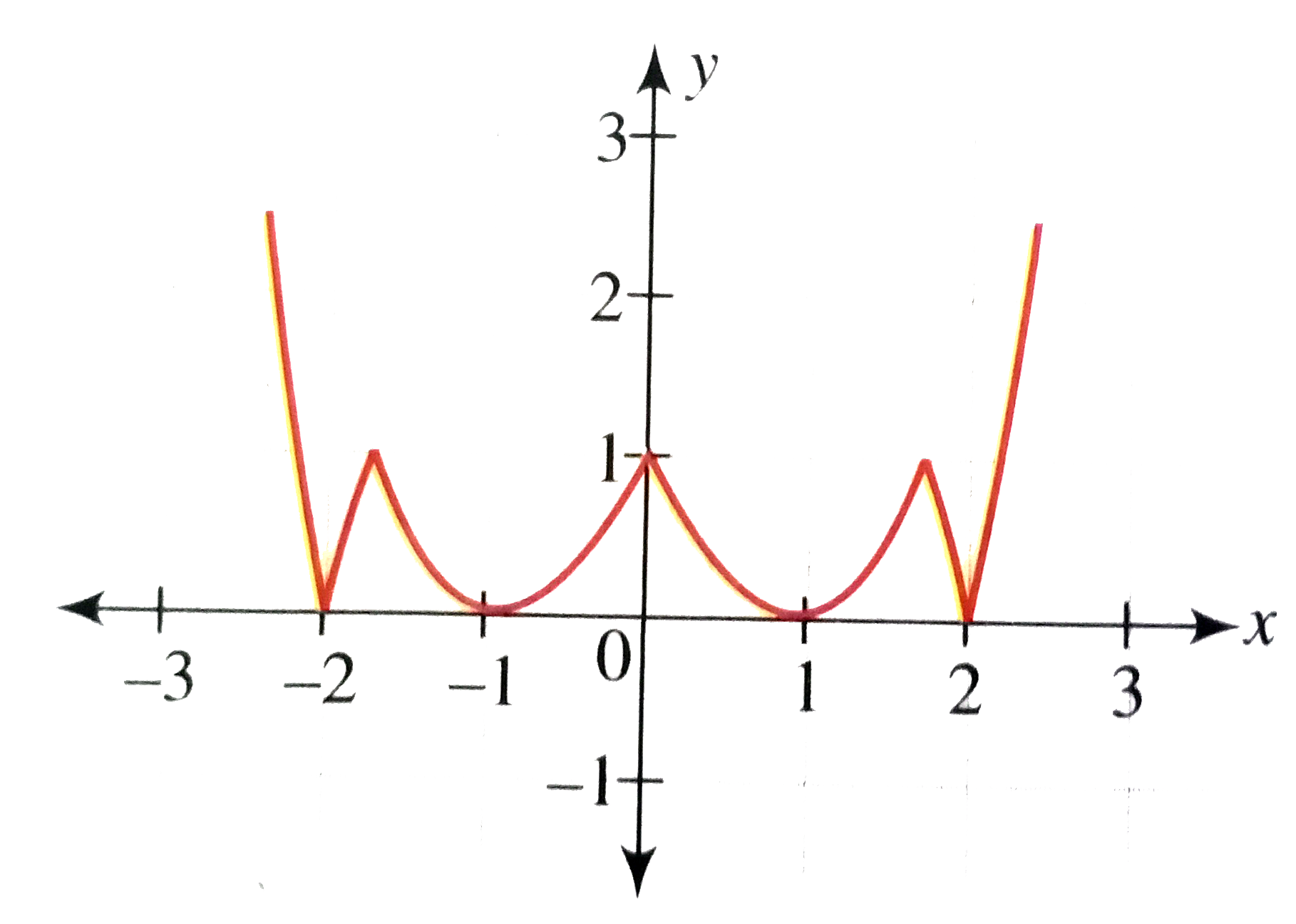
Now the line y=1/2 meets the above graph in eight points, hence the number of solutions is 8.
|
Topper's Solved these Questions
- GRAPHICAL TRANSFORMATIONSBOOK - CENGAGECHAPTER - GRAPHICAL TRANSFORMATIONSEXERCISE - Exercise
22 Videos
- GRAPH OF INVERSE TRIGONOMETRIC FUNCTIONSBOOK - CENGAGECHAPTER - GRAPH OF INVERSE TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise
18 Videos
- GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSBOOK - CENGAGECHAPTER - GRAPHS OF POLYNOMIAL AND RATIONAL FUNCTIONSEXERCISE - Exercise
13 Videos
Similar Questions
Knowledge Check
The graph of the function y = g(x) is shown. The number of solutions of the equationm ||g(x)|−1|=12, is
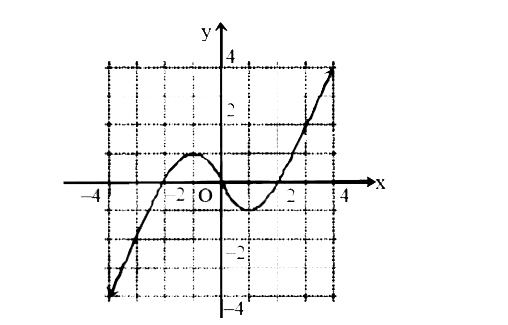 A4B5C6D8
A4B5C6D8The graph of y = f(x} is shown, then the number of solutions of f(f(x}} = 2 will be
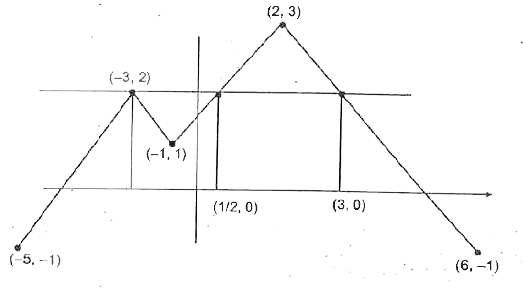 A1B2C3D4
A1B2C3D4
The graph of the function y=f(x) is shown in the adjacent figure then correct statement is
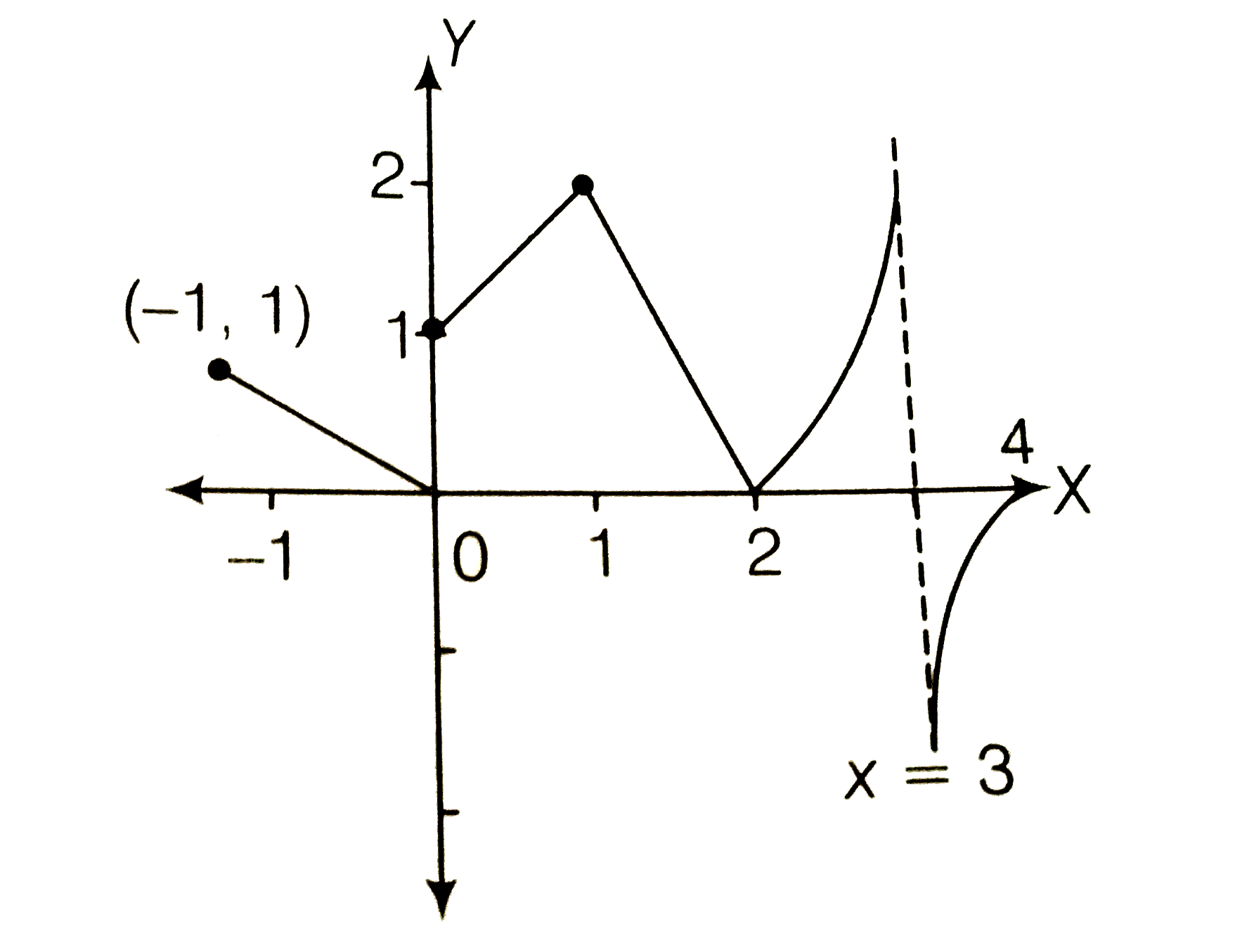
View SolutionIf f(x)=2x−1 then number of solution (s) of the equation |f(x)|=|f(|x|−1)| is (are)
View SolutionLet f(x)=x+sinx. Find the number of solutions of f(x)=f−1(x)
View SolutionFind the number of distinct real solutions of the equation f(f(f(x))=0, where f(x)=x2−1
View Solution(i) Determine whether f(x)=2x+34 for f:R→R is invertible or not If so find it.
(ii) Let f(x)=x2+2x,x≥−1 . Draw graph of f−1(x) also find the number of solutions of the equation f(x)=f−1(x)
(iii) If y=f(x)=x2−3x+2,x≤1.Find the value of g'(2) where g is inverse of f
View SolutionIf f(x)={0,x<1and2x−2,x≤1 then the number of solutions of the equation f(f(f(x)))=x is
View Solution
