The graph of the linear function f has intercepts at (c,0) and (0,d) in the xy-plane. If 2c=dandd≠0, which of the following in true about the slope of the graph of f ?
It is positive.
It is negative.
It equals zero.
It is underfined.
The correct Answer is:B
To solve the problem, we need to analyze the given information about the linear function f and its intercepts.
1. Identify the Intercepts:
The function f has intercepts at points (c,0) and (0,d). Here, c is the x-intercept and d is the y-intercept.
2. Use the Given Relationship:
We are given that 2c=d. This implies that the y-intercept d is twice the x-intercept c.
3. Determine the Signs of c and d:
Since d≠0, we can analyze two cases:
- Case 1: If d>0, then c must also be positive because d=2c implies c=d2>0.
- Case 2: If d<0, then c must also be negative because d=2c implies c=d2<0.
4. Graph the Function:
- In Case 1 (both c and d are positive), the line will be in the first quadrant.
- In Case 2 (both c and d are negative), the line will be in the third quadrant.
5. Calculate the Slope:
The slope m of the line can be calculated using the formula:
m=y2−y1x2−x1
For the intercepts (c,0) and (0,d):
m=d−00−c=d−c=−dc
6. Substituting d:
From the relationship d=2c, we substitute d into the slope formula:
m=−2cc=−2
7. Conclusion:
The slope of the graph of f is −2, which is negative.
Final Answer:
The slope of the graph of f is negative.
The function f has intercepts at points (c,0) and (0,d). Here, c is the x-intercept and d is the y-intercept.
We are given that 2c=d. This implies that the y-intercept d is twice the x-intercept c.
Since d≠0, we can analyze two cases:
- Case 1: If d>0, then c must also be positive because d=2c implies c=d2>0.
- Case 2: If d<0, then c must also be negative because d=2c implies c=d2<0.
- In Case 1 (both c and d are positive), the line will be in the first quadrant.
- In Case 2 (both c and d are negative), the line will be in the third quadrant.
The slope m of the line can be calculated using the formula:
m=y2−y1x2−x1
For the intercepts (c,0) and (0,d):
m=d−00−c=d−c=−dc
From the relationship d=2c, we substitute d into the slope formula:
m=−2cc=−2
The slope of the graph of f is −2, which is negative.
The slope of the graph of f is negative.
Topper's Solved these Questions
- FUNCTIONS BOOK - KAPLANCHAPTER - FUNCTIONS EXERCISE - FUNCTION NOTATION
1 Videos
- FUNCTIONS BOOK - KAPLANCHAPTER - FUNCTIONS EXERCISE - GRAPHS OF FUNCTIONS
1 Videos
- FUNCTIONS BOOK - KAPLANCHAPTER - FUNCTIONS EXERCISE - DESCRIBING REAL-LIFE SITUATIONS WITH FUNCTIONS
1 Videos
- EXPONENTS, RADICALS, POLYNOMIALS, AND RATIONAL EXPRESSIONSBOOK - KAPLANCHAPTER - EXPONENTS, RADICALS, POLYNOMIALS, AND RATIONAL EXPRESSIONSEXERCISE - RATIONAL EXPRESSIONS AND EQUATIONS
1 Videos
- GEOMETRY BOOK - KAPLANCHAPTER - GEOMETRY EXERCISE - THREE-DIMENSIONAL FIGURES
1 Videos
Similar Questions
Knowledge Check
The graph of the linear function f has intercepts at (a,0) and (0, b) in the xy-plane. If a+b=0 and a≠b, which of the following is true about the slope of the graph of f ?
AIt is positive.BIt is negative.CIt equals zero.DIt is undefined.In the xy-plane, the graph of which of the following equations is a line with a slope of 3 ?
Ay=13xBy = x − 3Cy = 3x + 2Dy = 6x + 3If function f has exactly two distinct real zeros, which of the following graphs could be the complete graph of f (x) ?
A B
B C
C D
D
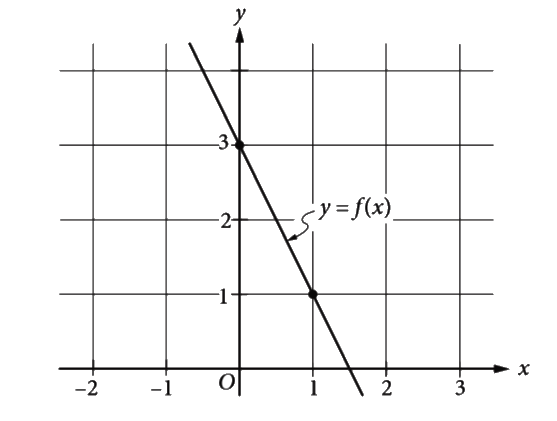
The graph of the linear function f is shown in the xy-plane above. The graph of the linear function g (not shown) is perpendicular to the graph of f and passes through the point (1,3). What is the value of g(0) ?
View Solution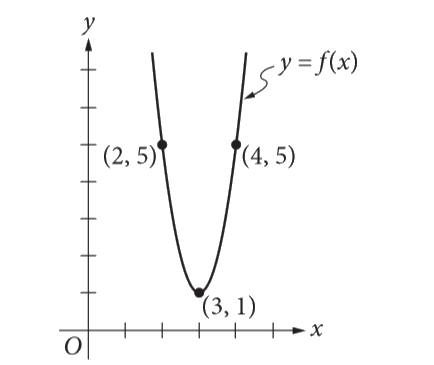
The graph of the function f in the xy-plane above is a parabola. Which of the following defines f ?
View SolutionIn the xy-plane, the graph of function f has x-intercepts at -3, -1, and 1. Which of the following could define f ?
View Solution12 If the function f has five distinct zeros, which of the following could represent the complete graph of f in the xy‑plane?
View SolutionIn the xy-plane, the graph of the polynomial function f crosses the x-axis at exactly two points, (a, 0) and (b, 0), where a and b are both positive. Which of the following could define f ?
View Solution