The line 6x+8y=48 intersects the coordinates axes at A and B, respecively. A line L bisects the area and the perimeter of triangle OAB, where O is the origin.
The slope of line L can be
(10+5√6)/10
(10−5√6)/10
(8+3√6)/10
none of these
The correct Answer is:B
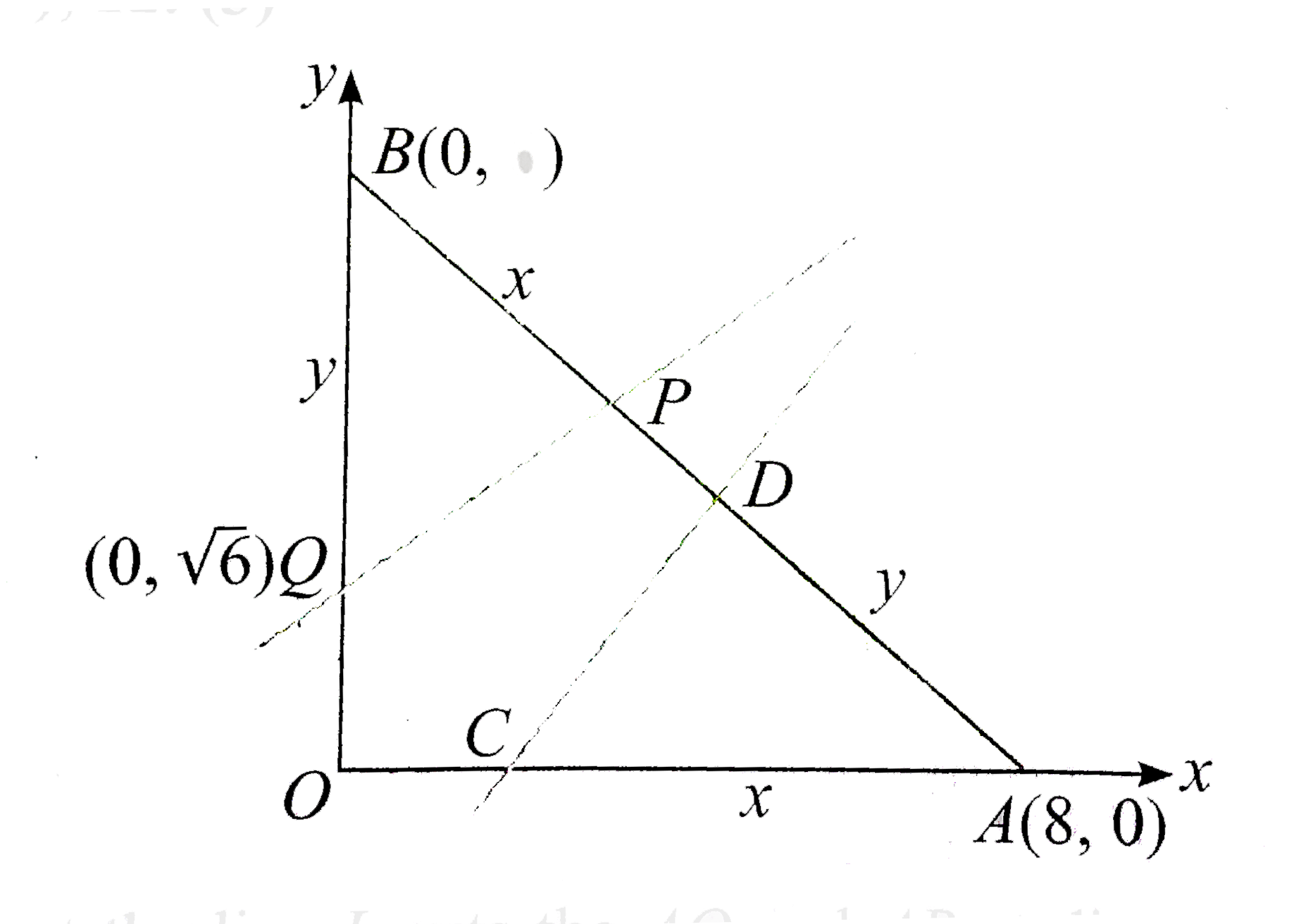
Case I : Let the line L cuts the AO and AB at distances x and y, respectively, from A. Then, the area of the triangle with sides x and y is
12xy sin(∠CAD)=12⋅xy⋅35=3xy10=12
or xy=40
Also, x+y=12 (from perimeter bisection). Then x and y are the roots of r2−12x+40=0 which has imaginary roots.
Case II: if the line L cuts OB and BA at distances y and x, respectively, from B, then we have xy=30 and x+y=12.
Solving, we get x=6+√6 and y=6−√6.
Case III: If the line L cuts the sides OA and OB at distances x and y, respectively, from O, then
x+y=12 and xy=24
∴x,y=6±2√3 (not possible)
So there is a unique line possible. Let point P be (α,β).
Using the parametric equation of AB, we have
β=6−35(6+√6)
and α=45(6+√6)
Hence, the slope of PQ is
β−√6α−0=10−5√610
Topper's Solved these Questions
- STRAIGHT LINESBook:CENGAGEChapter:STRAIGHT LINESExercise:Exercise (Matrix)
Explore 8 Videos
- STRAIGHT LINESBook:CENGAGEChapter:STRAIGHT LINESExercise:Exercise (Numerical)
Explore 13 Videos
- STRAIGHT LINESBook:CENGAGEChapter:STRAIGHT LINESExercise:Exercise (Multiple)
Explore 30 Videos
- STRAIGHT LINEBook:CENGAGEChapter:STRAIGHT LINEExercise:Multiple Correct Answers Type
Explore 8 Videos
- THEORY OF EQUATIONSBook:CENGAGEChapter:THEORY OF EQUATIONSExercise:JEE Advanced Previous Year
Explore 9 Videos
Similar Questions
The line 6x+8y=48 intersects the coordinates axes at A and B, respecively. A line L bisects the area and the perimeter of triangle OAB, where O is the origin.
Line L
View SolutionThe line 6x+8y=48 intersects the coordinates axes at A and B, respecively. A line L bisects the area and the perimeter of triangle OAB, where O is the origin.
The number of such lines possible is a. 1 b. 2 c. 3 d. 4
View Solution
Knowledge Check
The line 6x+8y=48 intersects the coordinates axes at A and B, respecively. A line L bisects the area and the perimeter of triangle OAB, where O is the origin.
Line LAdoes not intersect ABBdoes not intersect OBCdoes not intersect OADcan intersect all the sidesThe line 6x+8y=48 intersects the coordinates axes at A and B, respecively. A line L bisects the area and the perimeter of triangle OAB, where O is the origin.
The number of such lines possible isA1B2C3Dmore than 3The line 6x + 8y - 48 intersects the co - ordinate axis at A and B respectively. A line L bisects the area and the perimeter of the traingle OAB, where O is the origin .
The slope of the line L can beA(1−5√6)10B(10−5√6)10C(8+3√6)10Dnone of these
If the line 5x + 12y - 60 = 0 intersects the x-axis at the point A and the y-axis at the point B, then the incentre of the triangle OAB, where O is the origin, is:
View SolutionA variable line through point P(2,1) meets the axes at AandB . Find the locus of the circumcenter of triangle OAB (where O is the origin).
View SolutionA variable line through the point P(2,1) meets the axes at AandB . Find the locus of the centroid of triangle OAB (where O is the origin).
View SolutionThe line 6x + 8y - 48 intersects the co - ordinate axis at A and B respectively. A line L bisects the area and the perimeter of the traingle OAB, where O is the origin , the number of such lines possible is
View SolutionIf the line 5x + 12y - 60 = 0 intersects the x-axis at the point A and the y-axis at the point B, then the incentre of the triangle OAB, where O is the origin, is:
View Solution
