The line segments joining the midpoints of the adjacent sides of a quadrilateral form
a parallelogram
a rectangle
a square
a rhombus
The correct Answer is:A
To solve the problem of determining what the line segments joining the midpoints of the adjacent sides of a quadrilateral form, we can follow these steps:
1. Draw a Quadrilateral:
Start by drawing a quadrilateral ABCD. Label the vertices as A, B, C, and D.
Hint: Make sure to label the vertices clearly for reference in the next steps.
2. Identify Midpoints:
Find the midpoints of each side of the quadrilateral. Let P be the midpoint of side AB, Q be the midpoint of side BC, R be the midpoint of side CD, and S be the midpoint of side DA.
Hint: Use the midpoint formula if necessary, which is (x1+x2)/2,(y1+y2)/2.
3. Draw Line Segments:
Draw line segments joining the midpoints: PQ, QR, RS, and SP.
Hint: Ensure that you are connecting the midpoints in the correct order to form a closed shape.
4. Analyze Triangles:
Look at triangles formed by the vertices of the quadrilateral and the midpoints. For example, in triangle ABC, P and Q are midpoints of sides AB and BC, respectively.
Hint: Remember that the line segment joining the midpoints of two sides of a triangle is parallel to the third side and half its length.
5. Establish Parallel Lines:
From the previous step, since PQ is parallel to AC (the third side of triangle ABC) and RS is parallel to AC (in triangle ACD), we conclude that PQ is parallel to RS.
Hint: Use the properties of parallel lines and transversals to reinforce your conclusions.
6. Repeat for Other Triangles:
Now consider triangles ABD and BCD. You will find that PS is parallel to QR by similar reasoning.
Hint: Always check the relationships in both triangles to ensure consistency.
7. Conclude the Shape:
Since both pairs of opposite sides (PQ and RS, PS and QR) are parallel, we can conclude that the quadrilateral formed by the midpoints P, Q, R, and S is a parallelogram.
Hint: Remember that a quadrilateral is a parallelogram if both pairs of opposite sides are parallel.
Final Conclusion:
The line segments joining the midpoints of the adjacent sides of a quadrilateral form a parallelogram.
Start by drawing a quadrilateral ABCD. Label the vertices as A, B, C, and D.
Find the midpoints of each side of the quadrilateral. Let P be the midpoint of side AB, Q be the midpoint of side BC, R be the midpoint of side CD, and S be the midpoint of side DA.
Draw line segments joining the midpoints: PQ, QR, RS, and SP.
Look at triangles formed by the vertices of the quadrilateral and the midpoints. For example, in triangle ABC, P and Q are midpoints of sides AB and BC, respectively.
From the previous step, since PQ is parallel to AC (the third side of triangle ABC) and RS is parallel to AC (in triangle ACD), we conclude that PQ is parallel to RS.
Now consider triangles ABD and BCD. You will find that PS is parallel to QR by similar reasoning.
Since both pairs of opposite sides (PQ and RS, PS and QR) are parallel, we can conclude that the quadrilateral formed by the midpoints P, Q, R, and S is a parallelogram.
The line segments joining the midpoints of the adjacent sides of a quadrilateral form a parallelogram.
Topper's Solved these Questions
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - MULTPILE-CHOICE QUESTIONS (MCQ) ( MATCHING OF COLUMNS)
1 Videos
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - Test Yourself
20 Videos
- TRIANGLESBOOK - RS AGGARWALCHAPTER - TRIANGLESEXERCISE - Exercise 7E
30 Videos
- T-RATIOS OF SOME PARTICULAR ANGLESBOOK - RS AGGARWALCHAPTER - T-RATIOS OF SOME PARTICULAR ANGLESEXERCISE - Exercise 11
27 Videos
- TRIGONOMETRIC IDENTITIESBOOK - RS AGGARWALCHAPTER - TRIGONOMETRIC IDENTITIESEXERCISE - Test Yourself
20 Videos
Similar Questions
Knowledge Check
Assertion : ABCD and PQRC are rectangles and Q is a midpoint of AC. Then DP = PC.
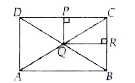
Reason : The line segment joining the midpoints of any two sides of a triangle is parallel to the third side and equal to half of it.AIf both assertion and reason are true and reason is the correct explanation of assertionBIf both assertion and reason are true but reason is not the correct explanation of assertion.CIf assertion is true but reason is false.DIf assertion is false but reason is true.The line segment joining the midpoints of any two sides of a triangle is parallel to the third side and equal to half of it.
In the given figure, the side AC of ΔABC is produced to E such that CE = FAC. If D is the midpoint of BC and ED produced meets AB at F and CP, DQ are drawn parallel to BA, then FD=
 A12FEB13EFC2FEDFE
A12FEB13EFC2FEDFE
The figure formed by joining the mid-points of the adjacent sides of a quadrilateral is a parallelogram (b) rectangle square (d) rhombus
View SolutionThe figure formed by joining the mid-points of the adjacent sides of a quadrilateral is a parallelogram (b) rectangle (c) square (d) rhombus
View SolutionShow that the line segments joining the mid-points of the opposite sides of a quadrilateral bisect each other.
View SolutionShow that the line segments joining the mid-points of the opposite sides of a quadrilateral bisect each other.
View SolutionShow that the line segments joining the mid-points of opposite sides of a quadrilateral bisects each other.
View SolutionArea of the quadrilaterals formed by joining the mid points of the adjacent sides of a quadrilateral is________ the area of given quadrilateral.
View Solution
