The maximum vlaue of Z=9x+13y subject to constraints 2x+3y≤18,2x+y≤10,x≥0,y≥0 is
A
130
B
81
C
79
D
28
Video Solution
Text Solution
The correct Answer is:C
The feasible region is OABCO.
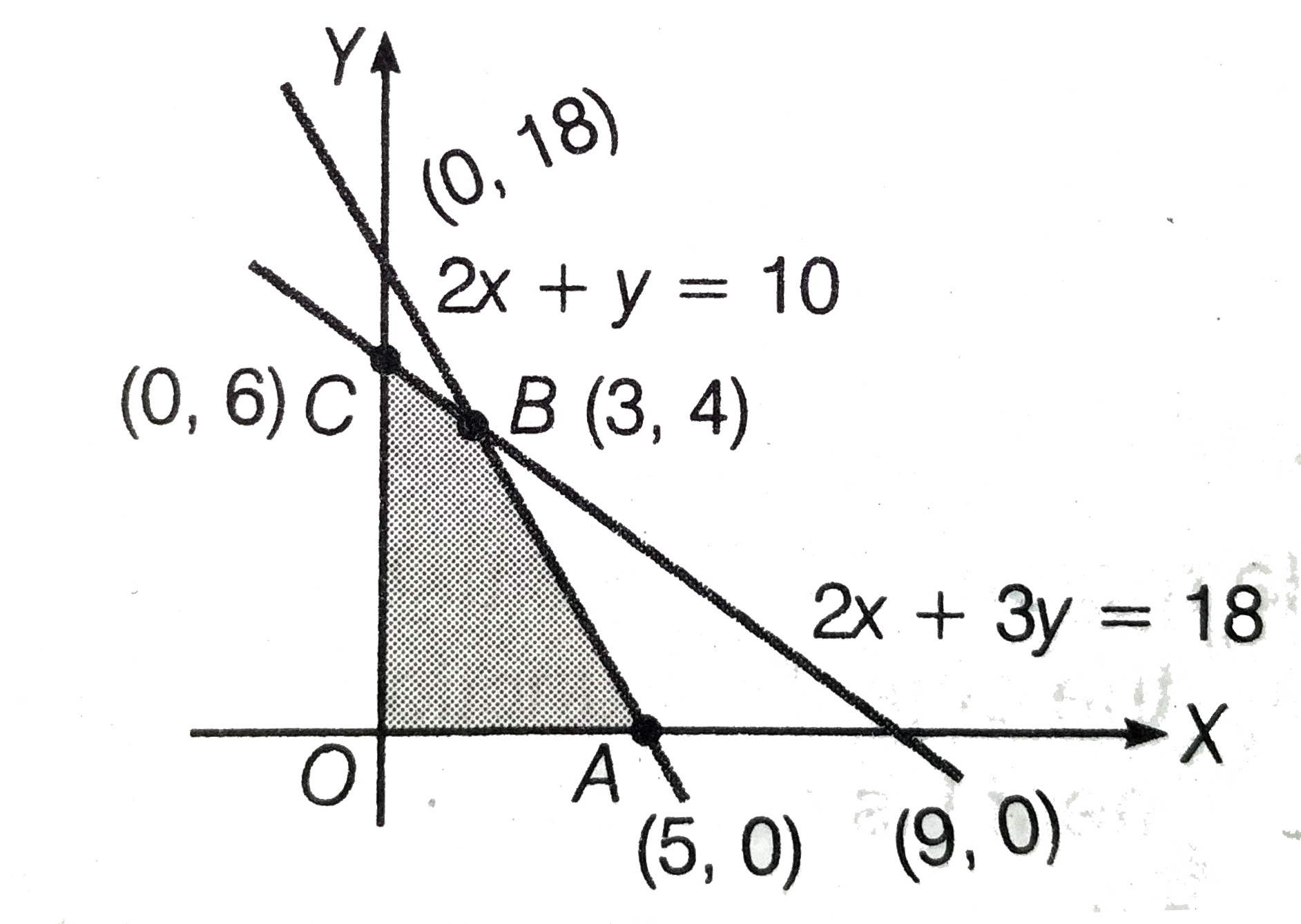
Now Z =9x+13y
At O(0,0) Z=0
At A(5,0) Z =45
At B(3,4) Z=27 +52 +79
At c(0,6) Z =78
∴ Maximum vlaue of Z is 79.
|
Updated on:21/07/2023
Topper's Solved these Questions
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - Linear Programming EXERCISE - EXERCISE 2 (MISCELLANEOUS PROBLEMS )30videos
Linear Programming
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - LINEEXERCISE - MHT CET Corner3videos
LINE
- BOOK - MHTCET PREVIOUS YEAR PAPERS AND PRACTICE PAPERSCHAPTER - MATHEMATICAL LOGIC EXERCISE - MHT CET CORNER22videos
MATHEMATICAL LOGIC
Similar Questions
Knowledge Check
- Question 1 - Select One
The maximum value of Z=9x+13y subject to constraints 2x+3y≤18,2x+y≤10,x≥0,y≥0, is
A130B81C79D99 - Question 2 - Select One
The maximum value of Z = 4x + 2y subject to the constraints 2x+3y≤18,x+y≥10,x,y≥0 is
A20B36C40DNone of these - Question 3 - Select One
The maximum value of z = 4x +2y subject to the constraints 2x+3y≤18,x+y≥10,x,y≥0 is
A40B20C35Dnone of these
The maximum value of Z = 4x + 2y subject to the constraints 2x+3y≤18,x+y≥10,x,y≥0 is
View SolutionThe maximum vlaue of Z=9x+13y subject to constraints 2x+3y≤18,2x+y≤10,x≥0,y≥0 is
View SolutionThe point at which the minimum value of z=8x+12y subject to the constraints 2x+y≥8,x+2y≥10x≥0,y≥0 is obtained is
View SolutionThe minimum value of Z=4x+5y subjected to the constraints x+y≥6,5x+y≥10,x≥0,y≥0 is
View SolutionThe maximum value of Z=3x+4y subject to the constraints:
x+y≤4,x≥0,y≥0 is :View Solution

