The mean of the following distribution is 52 and the frequency of class interval 30-40 is f. Find f.
The correct Answer is:4
To solve the problem step by step, we will first summarize the information given and then proceed to find the frequency f for the class interval 30-40.
Step 1: Understand the given data
We know that the mean of the distribution is 52. We also know that the frequency of the class interval 30-40 is f.
Step 2: Determine the mid-values of the class intervals
We need to find the mid-values for each class interval. Assuming the class intervals are as follows:
- 10-20
- 20-30
- 30-40
- 40-50
- 50-60
- 60-70
- 70-80
The mid-values Xi for these intervals are:
- For 10-20: 15
- For 20-30: 25
- For 30-40: 35
- For 40-50: 45
- For 50-60: 55
- For 60-70: 65
- For 70-80: 75
Step 3: Create a frequency table
Assuming the frequencies fi for the respective class intervals are:
- 10-20: 3
- 20-30: 3
- 30-40: f
- 40-50: 7
- 50-60: 2
- 60-70: 6
- 70-80: 13
Step 4: Calculate Σfi (Total frequency)
The total frequency Σfi can be calculated as:
Σfi=3+3+f+7+2+6+13=34+f
Step 5: Calculate Σ(Xifi) (Weighted sum of mid-values)
Now we calculate Σ(Xifi):
Σ(Xifi)=(15×3)+(25×3)+(35×f)+(45×7)+(55×2)+(65×6)+(75×13)
Calculating each term:
- 15×3=45
- 25×3=75
- 35×f=35f
- 45×7=315
- 55×2=110
- 65×6=390
- 75×13=975
Adding these together:
Σ(Xifi)=45+75+35f+315+110+390+975=1910+35f
Step 6: Set up the equation for the mean
Using the formula for the mean:
Mean=Σ(Xifi)Σfi
We know the mean is 52, so we set up the equation:
52=1910+35f34+f
Step 7: Cross-multiply to solve for f
Cross-multiplying gives:
52(34+f)=1910+35f
Expanding this:
1768+52f=1910+35f
Step 8: Rearranging the equation
Rearranging gives:
52f−35f=1910−1768
17f=142
Step 9: Solve for f
Dividing both sides by 17:
f=14217=8.3529
Since f must be a whole number, we can round it to the nearest integer, which is f=8.
Final Answer
The frequency f for the class interval 30-40 is approximately 8.
We know that the mean of the distribution is 52. We also know that the frequency of the class interval 30-40 is f.
We need to find the mid-values for each class interval. Assuming the class intervals are as follows:
- 10-20
- 20-30
- 30-40
- 40-50
- 50-60
- 60-70
- 70-80
- For 10-20: 15
- For 20-30: 25
- For 30-40: 35
- For 40-50: 45
- For 50-60: 55
- For 60-70: 65
- For 70-80: 75
Assuming the frequencies fi for the respective class intervals are:
- 10-20: 3
- 20-30: 3
- 30-40: f
- 40-50: 7
- 50-60: 2
- 60-70: 6
- 70-80: 13
The total frequency Σfi can be calculated as:
Σfi=3+3+f+7+2+6+13=34+f
Now we calculate Σ(Xifi):
Σ(Xifi)=(15×3)+(25×3)+(35×f)+(45×7)+(55×2)+(65×6)+(75×13)
Calculating each term:
- 15×3=45
- 25×3=75
- 35×f=35f
- 45×7=315
- 55×2=110
- 65×6=390
- 75×13=975
Σ(Xifi)=45+75+35f+315+110+390+975=1910+35f
Using the formula for the mean:
Mean=Σ(Xifi)Σfi
We know the mean is 52, so we set up the equation:
52=1910+35f34+f
Cross-multiplying gives:
52(34+f)=1910+35f
Expanding this:
1768+52f=1910+35f
Rearranging gives:
52f−35f=1910−1768
17f=142
Dividing both sides by 17:
f=14217=8.3529
Since f must be a whole number, we can round it to the nearest integer, which is f=8.
The frequency f for the class interval 30-40 is approximately 8.
Topper's Solved these Questions
- MEASURES OF CENTRAL TENDENCY (MEAN, MEDIAN, QUARTILES AND MODE)BOOK - ICSECHAPTER - MEASURES OF CENTRAL TENDENCY (MEAN, MEDIAN, QUARTILES AND MODE)EXERCISE - EXERCISE 24 (D)
8 Videos
- MATRICESBOOK - ICSECHAPTER - MATRICESEXERCISE - Exercise 9D
25 Videos
- MIXED PRACTICE BOOK - ICSECHAPTER - MIXED PRACTICE EXERCISE - SET B
52 Videos
Similar Questions
The mean of the following distribution is 18. Find the frequency f of the class 19−21.
View SolutionIf the mean of the following distribution is 7.5, find the missing frequency f

View SolutionThe mean of the following distribution is 50 but the frequency f1andf2 in classes 20-40 and 60-80, resepectively are not known. Find these frequencies, if the sum of all the fequencies is 120
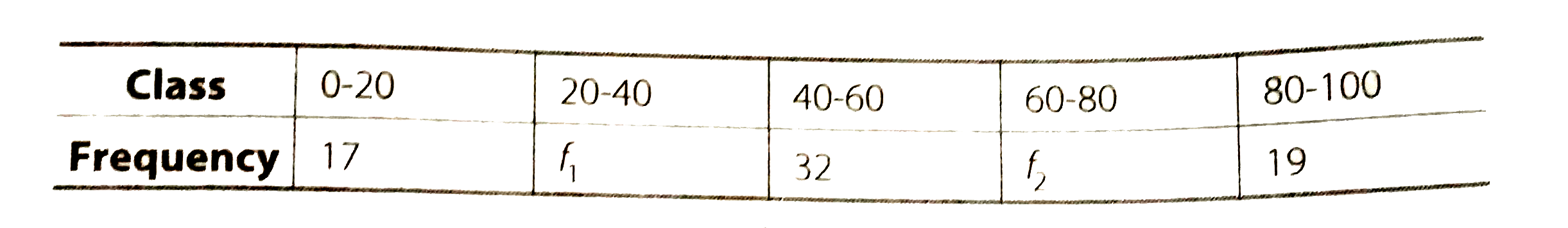
View SolutionWrite the comulative frequency of class interval 30-40

View SolutionThe mean of the following distribution is 62.8 and the sum of all the frequencies is 50. Find the missing frequencies f1 and f2

View SolutionThe mean of the following frequency distribution is 57.6 and the sum of the observations is 50. Find the missing frquencies f1andf2 :

View SolutionThe mean of the following frequency distribution is 2117. Find the value of f

View SolutionIf the median of the following frequency distribution is 28.5 find the missing frequencies: Class interval: 0-10 10-20 20-30 30-40 40-50 50-60 Total Frequency: 5 f1 20 15 f2 5 60
View SolutionIf the mean of the following distribution is 54, find the value of p: Class: 0-20 20-40 40-60 60-80 80-100 Frequency: 7 p 10 9 13
View SolutionThe mean of the following frequency distribution is 50, but the frequencies f1andf2 in class 20-40 and 60-80 respectively are not known. Find these frequencies.

Given that the sum of frequencies is 120.
View Solution
