The number of roots of the equation xsinx=1,x∈[−2π,0)∪(0,2π) is 2 (b) 3 (c) 4 (d) 0Solution in Tamil
We have x sin x = 1
∴ sinx=1x
Number of roots of the above equation = number of points (s) of the intersection of the graphs of y=sinx and y=1x for x∈[−2π,0)∪(0,2π]
The graphs of both functions are as shown in the following figure.
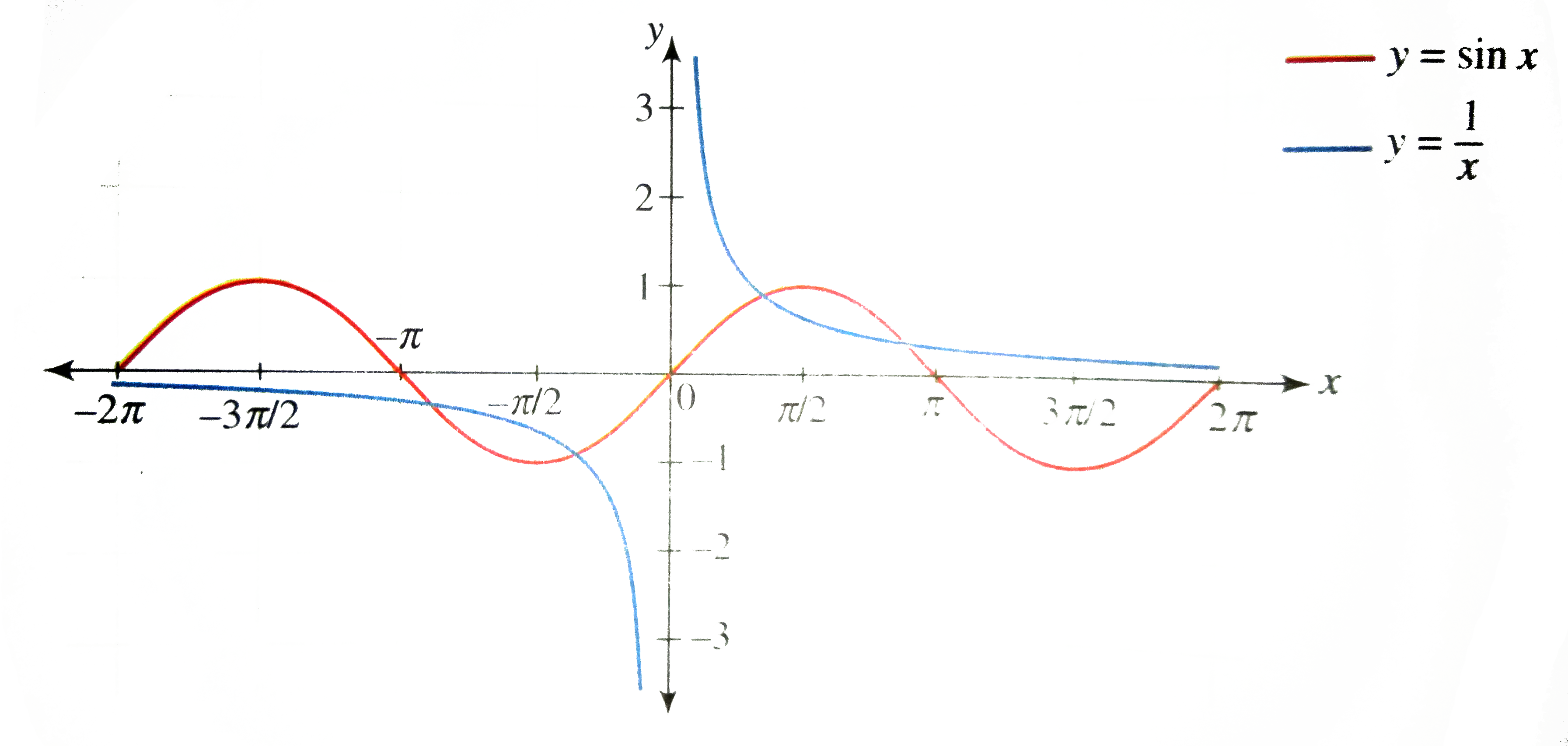
Graphs intersect at four points, hence four roots.
Topper's Solved these Questions
- GRAPHS OF TRIGONOMETRIC FUNCTIONSBOOK - CENGAGECHAPTER - GRAPHS OF TRIGONOMETRIC FUNCTIONSEXERCISE - Exercise
22 Videos
- GRAPHS OF ELEMENTARY FUNCTIONS BOOK - CENGAGECHAPTER - GRAPHS OF ELEMENTARY FUNCTIONS EXERCISE - Exercise
34 Videos
- HIGHT AND DISTANCE BOOK - CENGAGECHAPTER - HIGHT AND DISTANCE EXERCISE - JEE Previous Year
3 Videos
Similar Questions
Draw the graph of y= cosec 2x−cot2x. Is f(x) periodic ? If yes, what is its fundamental period ?
View SolutionDraw the graph of y=1(1/x).
View SolutionA bird is sitting on the top of a vertical pole 20 m high and its elevation from a point O on the ground is 45o . It flies off horizontally straight away from the point O. After one second, the elevation of the bird from O is reduced to 30o . Then the speed (in m/s) of the bird is (1) 40(√2−1) (2) 40(√3−2) (3) 20√2 (4) 20(√3−1)
View SolutionThe number of roots of the equation xsinx=1,x∈[−2π,0)∪(0,2π] is 2 (b) 3 (c) 4 (d) 0
View SolutionThe number of real roots (s) of the equation x2tanx=1 lying between 0 and 2π is /are (A) 1 (B) 2 (C) 3 (D) 4
View SolutionFind the number of roots of the equation xsinx=1,x∈[−2π,0)∪(0,2π].
View SolutionThe number of roots of the equation xsinx=1,,x∈[−2π,0]∪(0,2π) is
View SolutionThe number of solutions of the equation tanx+secx=2cosx lying in the interval [0,2π] is 0 (b) 1 (c) 2 (d) 3
View SolutionThe number of roots of the equation xsinx=1,x∈[−2π,0)∪(0,2π] is (a) 2 (b) 3 (c) 4 (d) 0
View SolutionIf the roots of the equation x2+ax+b=0arecandd, then roots of the equation x2+(2c+a)x+c2+ac+b=0 are a c b. d−c c. 2c d. 0
View SolutionFind the number of roots of the equation xsinx=1,x∈[−2π,0)∪(0,2π].
View SolutionIf |cotx+cosecx|=|cotx|+|cosecx|,x∈[0,2π], then complete set of values of x is : (a).[0,π] (b).(0,π2] (c).(0,π2]∪[3π2,2π) (d).(π,3π2]∪[7π4,2π]
View SolutionNumber of roots of equation 3|x|−|2−|x∣∣=1 is a. 0 b. 2 c. 4 d. 7
View SolutionThe number of solution of equation 2cos−1x=a+a2(cos−1x)−1 are at least (a) 1 if a∈[−2π,π]−{0} (b) 1 if a ∈(0,π] (c) 1 if a∈[−2π,0) (d) 2 if a>0
View SolutionNumber of roots of equation 3|x|−|2−|x∣∣=1 is a. 0 b. 2 c. 4 d. 7
View SolutionThe number of real roots of the equation x2tanx=1 lies between 0and2π is/are
(A) 1 (B) 2 (C) 3 (D) 4
View Solution
