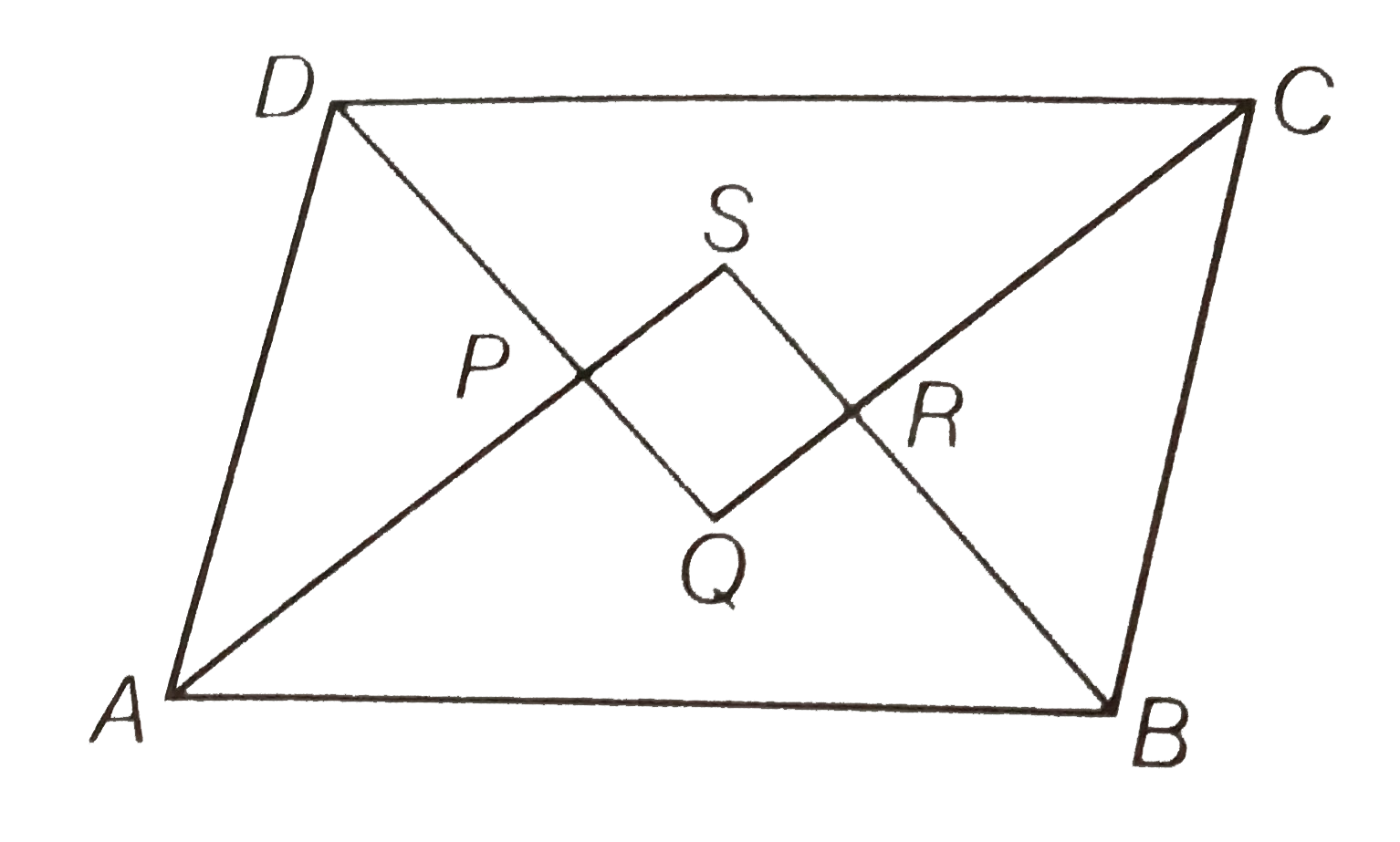
The quadrilateral formed by the bisectors of the angles of a parallelogram is a
A
Trapezium
B
Kite
C
Rectangle
D
None
Video Solution
Text Solution
The correct Answer is:C
Given Let ABCD be a parallelogram and AP, BR, CR, be are the bisectors of ∠A,∠B,∠Cand∠D, respectively.
To prove Quadrilateral PQRS is a rectangle.
Proof Since, ABCD is a parallelogram, then DC||AB and DA is a transversal.
We have, ∠A+∠D=180∘
[sum of cointerior angles of parallelogram is 180∘]
⇒ 12∠A+12∠D=90∘ [dividing both sides by 2]
⇒ ∠PAD+∠PDA=90∘ ltBrgt ⇒ ∠APD=90∘ [since, sum of all angles of a triangle is 180∘]
∴ ∠SPQ=90∘ [vertically opposite angles]
Similarly, ∠PQR=90∘
∠QRS=90∘
and ∠PSR=90∘
Thus, PQRS is a quadrilateral whose each angle is 90∘.
Hence, PQRS is a rectangle. Hence proved.
|
Topper's Solved these Questions
Similar Questions
Knowledge Check
The bisector of the angles of a parallelogram enclose a
ArectangleBrhombusCsquareDtrapeziumShape made by the bisectors of angles of a parallelogram is
ARectangleBSquareCCircleDStraight lineTwo parallel line l and m are intersected by a transversal p. The quadrilateral formed by the bisectors of interior angles is a
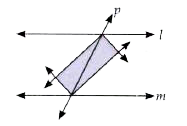 ATrapeziumBKiteCParallelogramDSquare
ATrapeziumBKiteCParallelogramDSquare
The quadrilateral formed by angle bisectors of a cyclic quadrilateral is also cyclic.
View SolutionThe quadrilateral formed by angle bisectors of a cyclic quadrilateral is also cyclic.
View SolutionThe bisector of the angles of a parallelogram enclose a ..................
View SolutionThe quadrilateral formed by the bisectors of the angles of a parallelogram is a

View SolutionThe quadrilateral formed by the bisectors of the angles of a parallelogram is a

View Solution
