The record of a weather station shows that out of the past 250 consecutive days, its weather forecast were correct 175 times. What is the probability that on a given day (i) it was correct? (ii) it was not correct?
To solve the problem, we need to calculate the probability that the weather forecast was correct and the probability that it was not correct based on the given data.
1. Identify the Total Number of Days:
The total number of days recorded is given as 250 days.
2. Identify the Number of Correct Forecasts:
The number of days the weather forecast was correct is given as 175 days.
3. Calculate the Probability that the Forecast was Correct:
The probability (P) that the forecast was correct can be calculated using the formula:
P(Correct)=Number of Correct ForecastsTotal Number of Days=175250
Now, simplify the fraction:
P(Correct)=175÷25250÷25=710=0.7
4. Calculate the Number of Incorrect Forecasts:
To find the number of days the forecast was not correct, subtract the number of correct forecasts from the total number of days:
Number of Incorrect Forecasts=250−175=75
5. Calculate the Probability that the Forecast was Not Correct:
The probability that the forecast was not correct can be calculated using the formula:
P(Not Correct)=Number of Incorrect ForecastsTotal Number of Days=75250
Now, simplify the fraction:
P(Not Correct)=75÷25250÷25=310=0.3
Final Answers:
(i) The probability that the weather forecast was correct is 0.7.
(ii) The probability that the weather forecast was not correct is 0.3.
The total number of days recorded is given as 250 days.
The number of days the weather forecast was correct is given as 175 days.
The probability (P) that the forecast was correct can be calculated using the formula:
P(Correct)=Number of Correct ForecastsTotal Number of Days=175250
Now, simplify the fraction:
P(Correct)=175÷25250÷25=710=0.7
To find the number of days the forecast was not correct, subtract the number of correct forecasts from the total number of days:
Number of Incorrect Forecasts=250−175=75
The probability that the forecast was not correct can be calculated using the formula:
P(Not Correct)=Number of Incorrect ForecastsTotal Number of Days=75250
Now, simplify the fraction:
P(Not Correct)=75÷25250÷25=310=0.3
(i) The probability that the weather forecast was correct is 0.7.
(ii) The probability that the weather forecast was not correct is 0.3.
Topper's Solved these Questions
Similar Questions
The record of a weather station shows that out of the past 250 onsecutivedays, its weather forecasts were correct 175 times.(i) What is the probability that on a given day it was correct?(ii) What is the probability that it was not correct on a given day?
View SolutionIn a school, 300 students were surveyed. The survey showed that 186 students liked watching cricket match while the rest disliked it. Out of these students, if one student is chosen at random, what is the probability that the chosen student :
(i) likes watching cricket match?
(ii) dislikes watching cricket match?View Solution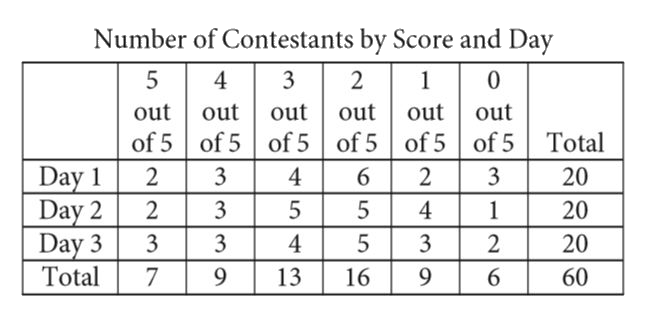
The same 20 contestants, on each of 3 days, answered 5 questions in order to win a prize. Each contestant received 1 point for each correct answer. The number of contestants receiving a given score on each day is shown in the table above.
No contestant received the same score on two different days. If a contestant is selected at random, what is the probability that the selected contestant received a score of 5 on Day 2 or Day 3, given that the contestant received a score of 5 on one of the three days?View SolutionTwo dice are thrown simultaneouly 500 times. Each time the sum of the two numbers appearing on their tops is noted and recorded as given in the following table

If the dice are thrown once more, then what is probability of getting a sum
i) 3?
ii) More than 10?
iii) Less than or equal to 5?
iv) Between 8 and 12?View SolutionTwo customers Shyam and Ekta are visiting a particular shop in the same week (Tuesday to Saturday). Each is equally likely to visit the shop on any day as on another day. What is the probability that both will visit the shop on (i) the same day? (ii) consecutive days? (iii) different days?
View SolutionOn a particular day, at a crossing in a city, the various types of 280 vehicles going past during a time interval were observed as under:
∣∣∣Type of vehicleTwo wheelersThree wheelersFour wheelersFrequency 91 63 126∣∣∣
Out of these vechicles , one is chosen at random, what is the probability that the chosen vechicle is
(i) a four wheeler
(ii) a two wheeler
(iii) a three wheeler?View Solution. In a class test containing 10 questions, 5 marks are awarded for every correct answer and (−2) marks are awarded for every incorrect answer and 0 for questions not attempted. (i) Mohan gets four correct and six incorrect answers. What is his score? (ii) Reshma gets five correct answers and five incorrect answers, what is her score? (iii) Heena gets two correct and five incorrect answers out of seven questions she attempts. What is her score?
View Solution(i) Show dimensionally that the equation of the time period of a simple pendulum of length l. Given relation T=2πl/g is incorrect.
(ii) Find its correct form.View Solution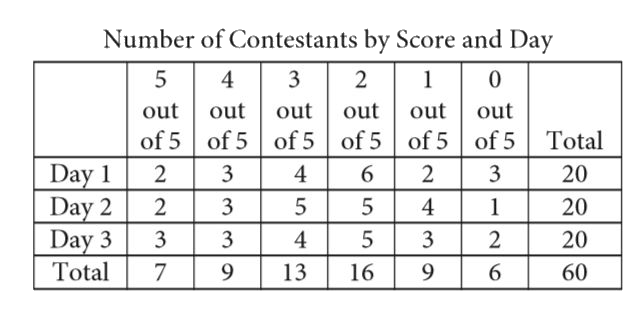
The same 20 contestants, on each of 3 days, answered 5 questions in order to win a prize. Each contestant received 1 point for each correct answer. The number of contestants receiving a given score on each day is shown in the table above.
What was the mean score of the contestants on Day 1 ?View SolutionGiven that T stands for time period nd 1 stands for the length of simple pendulum. If g is the acceleration due to gravity, then which of the following statements about the relation T2=lg is correct ?
(I) It is correct both dimensionally as well unmerically
(II) It is neither dimensionally correct nor numerically
(III) It is dimensionally correct but not numerically
(IV) It is numerically correct but not dimensionallyView Solution

