The side BC of ΔABC is product to N. bisector of angle meets BC at M. Prove that ∠ABC+∠ACN=2∠AMC
To prove that ∠ABC+∠ACN=2∠AMC in triangle ΔABC where side BC is produced to point N and the bisector of angle A meets BC at M, we can follow these steps:
1. Draw the Triangle and Extend Side BC:
- Draw triangle ABC with points A, B, and C.
- Extend side BC to point N.
2. Identify Angles:
- Let ∠BAM=∠1 (since AM is the angle bisector).
- Therefore, ∠CAM=∠1 as well.
- Let ∠ABC=∠2.
- Let ∠ACN=∠4.
- Let ∠AMC=∠3.
3. Apply the Exterior Angle Theorem:
- In triangle AMC, the exterior angle ∠ACN (which is ∠4) is equal to the sum of the opposite interior angles:
∠ACN=∠AMC+∠BAM
Thus, we can write:
∠4=∠3+∠1(Equation 1)
4. Apply the Exterior Angle Theorem Again:
- In triangle ABM, the exterior angle ∠AMC (which is ∠3) is equal to the sum of the opposite interior angles:
∠AMC=∠ABC+∠BAM
Thus, we can write:
∠3=∠2+∠1(Equation 2)
5. Substitute Equation 2 into Equation 1:
- Substitute ∠3 from Equation 2 into Equation 1:
∠4=(∠2+∠1)+∠1
This simplifies to:
∠4=∠2+2∠1
6. Combine the Angles:
- From the above equation, we can express ∠2+∠4:
∠2+∠4=∠2+(∠2+2∠1)=2∠2+2∠1
7. Relate to 2∠AMC:
- Since ∠3=∠1 (because AM is the angle bisector), we have:
2∠1=2∠AMC
- Therefore, we conclude:
∠ABC+∠ACN=2∠AMC
Conclusion
Thus, we have proved that:
∠ABC+∠ACN=2∠AMC
- Draw triangle ABC with points A, B, and C.
- Extend side BC to point N.
- Let ∠BAM=∠1 (since AM is the angle bisector).
- Therefore, ∠CAM=∠1 as well.
- Let ∠ABC=∠2.
- Let ∠ACN=∠4.
- Let ∠AMC=∠3.
- In triangle AMC, the exterior angle ∠ACN (which is ∠4) is equal to the sum of the opposite interior angles:
∠ACN=∠AMC+∠BAM
Thus, we can write:
∠4=∠3+∠1(Equation 1)
- In triangle ABM, the exterior angle ∠AMC (which is ∠3) is equal to the sum of the opposite interior angles:
∠AMC=∠ABC+∠BAM
Thus, we can write:
∠3=∠2+∠1(Equation 2)
- Substitute ∠3 from Equation 2 into Equation 1:
∠4=(∠2+∠1)+∠1
This simplifies to:
∠4=∠2+2∠1
- From the above equation, we can express ∠2+∠4:
∠2+∠4=∠2+(∠2+2∠1)=2∠2+2∠1
- Since ∠3=∠1 (because AM is the angle bisector), we have:
2∠1=2∠AMC
- Therefore, we conclude:
∠ABC+∠ACN=2∠AMC
Thus, we have proved that:
∠ABC+∠ACN=2∠AMC
Topper's Solved these Questions
- LINES AND ANGLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - LINES AND ANGLESEXERCISE - Revision Exercise (very Short Answer Questions )
10 Videos
- LINES AND ANGLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - LINES AND ANGLESEXERCISE - Revision Exercise (short Answer Questions)
12 Videos
- LINES AND ANGLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - LINES AND ANGLESEXERCISE - Exercise 6 B
16 Videos
- LINEAR EQUATIONS IN TWO VARIABLESBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - LINEAR EQUATIONS IN TWO VARIABLESEXERCISE - Revision Exercise
12 Videos
- NUMBER SYSTEMBOOK - NAGEEN PRAKASHAN ENGLISHCHAPTER - NUMBER SYSTEMEXERCISE - Revision Exercise (short Answer Questions)
10 Videos
Similar Questions
ABC is a right triangle with AB = AC.If bisector of ∠A meet BC at D then prove that BC =2 AD .
View SolutionIn triangle ABC,the bisector of interior angle A and the bisector angle C meet at point O. Prove that ∠AOC=12∠B
View SolutionIn parallelogram ABCD, the bisector of angle A meets DC at P and AB= 2AD. Prove that:
BP bisects angle B
View SolutionIn parallelogram ABCD, the bisector of angle A meets DC at P and AB= 2AD. Prove that:
Angle APB= 90∘
View SolutionIn a tringle ABC, AB = AC and bisector of angle A meets BC at D. Prove that :
(i) ΔABD≅ΔACD (ii) AD is perpendicular to BC.
View SolutionIn triangle ABC, D is mid-point of AB and CD is perpendiicular to AB. Bisector of ∠ABC meets CD at E and AC at F. Prove that:
F is equidistant from AB and BC.
View SolutionTriangle ABC is similar to triangle PQR. If bisector of angle BAC meets BC at point D and bisector of angle QPR meets QR at point M, prove that : ABPQ=ADPM
View SolutionIn the given PR is the bisector of ∠BPC.It meets BC and AD at points Q and R respectively. Prove that:
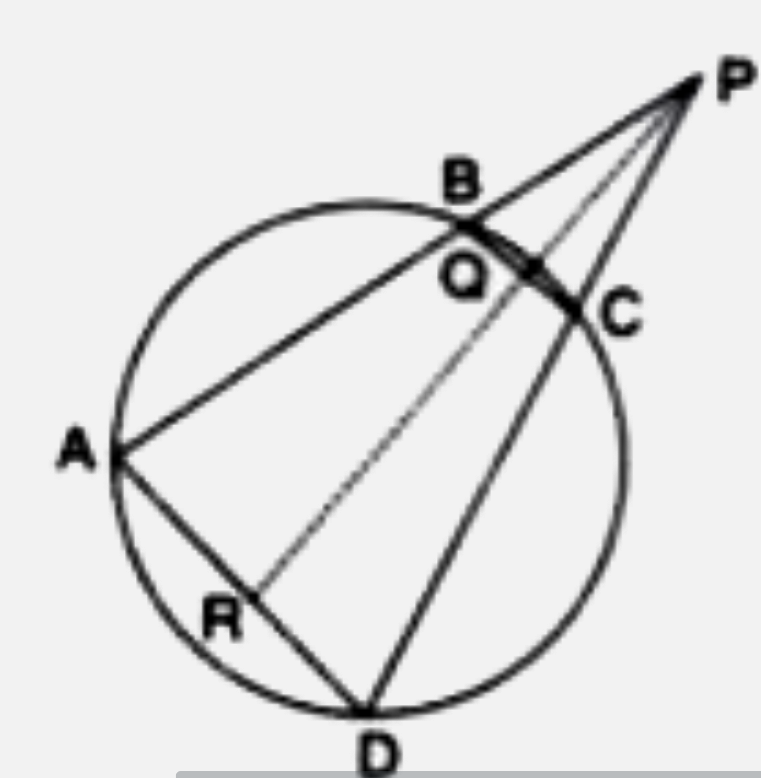
∠ARQ=∠BQR
View SolutionIn a triangle ABC , AB = AC and ∠A=36∘ If the internal bisector of angle C meets AB at D . Prove that AD = BC.
View SolutionIn the given PR is the bisector of ∠BPC.It meets BC and AD at points Q and R respectively. Prove that:

angle ARQ + angle RQC = 180^(@)
View Solution
