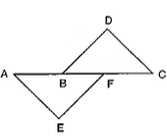
The sides BC, CA and AB of a ABC, are produced in order, forming exterior angles ∠ACD, ∠BAE and ∠CBF. Show that ∠ACD+ ∠BAE+ ∠CBF=3600
Solution:
∠ABC+∠CBF=180∘[Linear pair]………..(i)
∠ACB+∠ACD=180∘ [Linear pair]……(ii)
∠BAC+∠BAE=180∘
[Linear pair]…….(iii)
By adding(i), (ii) and (iii)
∠ABC+∠CBF+∠ACB+∠ACD+∠BAC+∠BAE=180+180+180
∠ABC+∠ACB+∠BAC+∠CBF+∠ACD+∠BAE=540∘
180+∠CBF+∠ACD+∠BAE=540∘[Sum of the angles of a triangle 180∘]
∠CBF+∠ACD+∠BAE=360∘
Topper's Solved these Questions
Similar Questions
D, E, F are the mid-point of the sides BC, CA and AB respectively of ABC. Then DEF is congruent to triangle. ABC (b) AEF (c) BFD, CDE (d) AFE, BFD, CDE
Given : D, E, F are the mid-point of the sides BC, CA and AB .
View SolutionIn Figure, it is given that AB=CF, EF=BD and ∠AFE= ∠CBD. Prove that AFE= ≅CBD
 View Solution
View SolutionIn Fig.81, side BC of ABC has been produced to D and CEBA. If ∠ABC=650, ∠BAC=550, find ∠ACE, ∠ECD and ∠ACD.
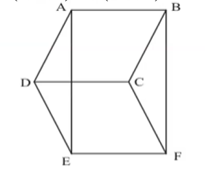
View SolutionIn Figure, ABCD, ABFE and CDEF are parallelograms. Prove that ar(ADE)=ar(BCF)
 View Solution
View SolutionIf ABCD is a rhombus with ∠ABC=56∘, find the measure of ∠ACD
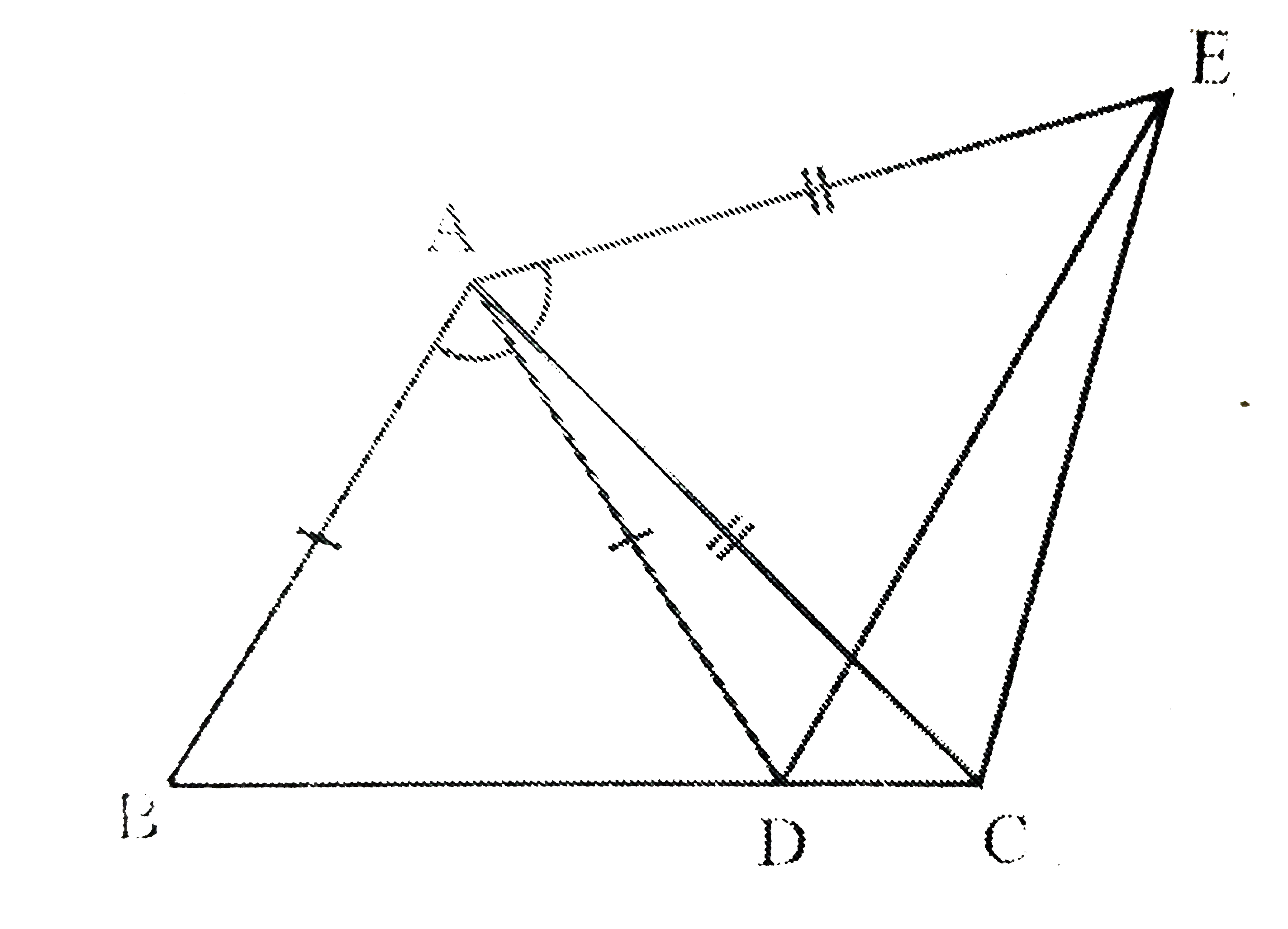
View SolutionIn Fig. 7.21, AC = AE, AB = ADand ∠BAD =∠EAC. Show that BC = DE.
 View Solution
View SolutionIn Fig. 71, if ABCD and CDEF, find ∠ACE
View SolutionThe sides AB and CD of a parallelogram ABCD are bisected at E and F. Prove that EBFD is a parallelogram.
View SolutionIn a parallelogram ABCD, the diagonals bisect each other at O. If ∠ABC=300, ∠BDC=100and ∠CAB=700, Find: ∠DAB, ∠ADC, ∠BCD, ∠AOD, ∠DOC, ∠BOC, ∠AOB, ∠ACD, ∠CAB, ∠ADB
Given that
∠ABC=302,∠ABC=∠ADC=300
[We know that measure of opposite angles are equal in a parallelogram]
∠BDC=100
∠CAB=700
∠BDA=∠ADB=∠ADC–∠BDC
302–102=202
∠DAB=1800–300=1500
∠ADB=∠DBC=200 (alternate angles)
∠BCD=∠DAB=1500
[we know, opposite angles are equal in a parallelogram]
∠DBA=∠BDC=100
[we know, Alternate interior angles are equal]
InΔABC
∠CAB+∠ABC+∠BCA=1800
[since, sum of all angles of a triangle is 180^0]
700+300+∠BCA=1800
∠BCA=1800–1000=800
∠DAB=∠DAC+∠CAB=700+800=1500
∠BCD=1500 (opposite angle of the parallelogram)
∠DCA=∠CAB=700
In ΔDOC∠BDC+∠ACD+∠DOC=1800
[since, sum of all angles of a triangle is 180^0]
100+700+∠DOC=1800
∠DOC=1800−800
∠ACB=800View SolutionThe side BC of ABC is produced to a point D. The bisector of ∠A meets side BC in L. If ∠ABC=300and ∠ACD=1150, then ∠ALC= 850 (b) 72120 (c) 1450 (d) none of these
View Solution

