The straight line 3x+4y−12=0 meets the coordinate axes at AandB . An equilateral triangle ABC is constructed. The possible coordinates of vertex C (2(1−3√34),32(1−4√3)) (−2(1+√3),32(1−√3)) (2(1+√3),32(1+√3)) (2(1+3√34),32(1+4√3))
(2(1−3√34),32(1−4√3))
(−2(1+√3),32(1−√3))
(2(1+√3),32(1+√3))
(2(1+3√34),32(1+4√3))
The correct Answer is:A, D
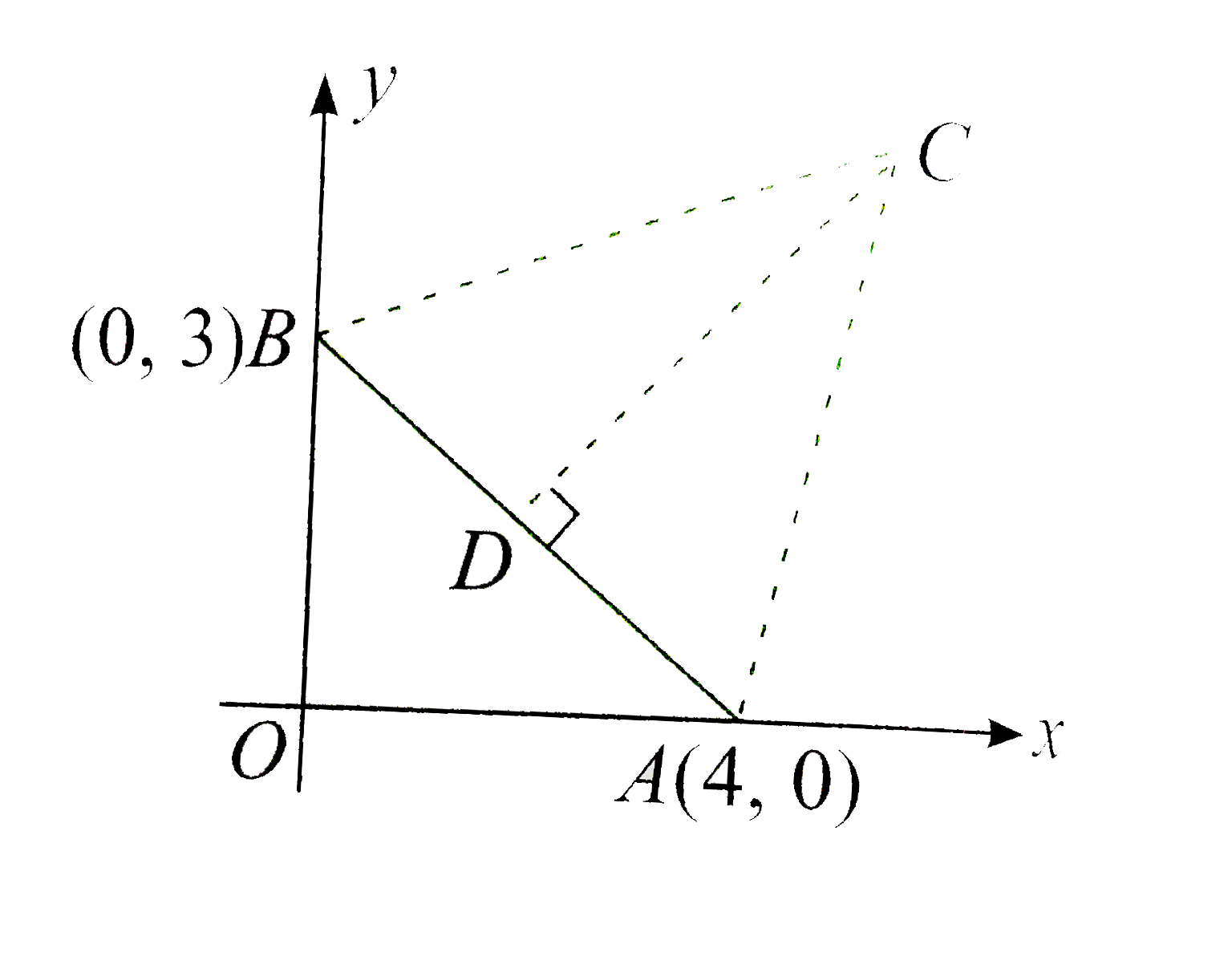
AB =5, D≡(2,32)
CD=5×√32=5√32
Slope of AB=−34
Slope of CD =34
If C≡(h,k),then
h−23/5=k−3/24/5=±5√32
or h=2(1−3√34),k=32(1−4√3)
or h=2(1+3√34),k=32(1+4√3)
Topper's Solved these Questions
- BOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - EXERCISE (LINKED COMPREHENSION TYPE)27videos
STRAIGHT LINES
- BOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - EXERCISE (MATRIX MATCH TYPE)8videos
STRAIGHT LINES
- BOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - EXERCISE (SINGLE CORRECT ANSWER TYPE)82videos
STRAIGHT LINES
- BOOK - CENGAGE ENGLISHCHAPTER - STRAIGHT LINEEXERCISE - Multiple Correct Answers Type8videos
STRAIGHT LINE
- BOOK - CENGAGE ENGLISHCHAPTER - THEORY OF EQUATIONSEXERCISE - JEE ADVANCED (Numerical Value Type )1videos
THEORY OF EQUATIONS
Similar Questions
The straight line 3x+4y−12=0 meets the coordinate axes at AandB . An equilateral triangle ABC is constructed. The possible coordinates of vertex C (a) (2(1−3√34),32(1−4√3)) (b)(−2(1+√3),32(1−√3)) (c)(2(1+√3),32(1+√3)) (d)(2(1+3√34),32(1+4√3))
View Solution√3+1+√3+12√2
View Solution12√5−√3−2√5+√32√5+√3=
View Solution√3−√2√3+√2−√3+√2√3−√2+1√2+1−1√2−1
View Solution(√3−1)+12(√3−1)2+13(√3−1)3+….∞
View Solution[(√2+i√3)+(√2−i√3)][(√3+1√2)+(√3−1√2)]
View SolutionLet A=[√3−12+√31−√3],B=[−√322−√31+√3] Find A+B.
View SolutionSimplify : 1√3+√2−1√3−√2+2√2+1
View SolutionFor all n∈N,1+1√2+1√3+1√4++1√n
View SolutionAngles of a triangle are in 4:1:1 ration. The ratio between its greatest side and perimeter is 32+√3 (b) √32+√3 √32−√3 (d) 12+√3
View Solution

