The table shows some values of the linear functions f and and g. If h(n)=2×f(n)−g(n), what is the value of h(6) ?
A
21.3
B
35.0
C
41.1
D
42.1
Text Solution
The correct Answer is:D
Determine the linear change of the functions relative to the change in n, then extrapolate to get the values of f (6) and g (6). You don't need to determine the actual expressions for the functions. As a shortcut, find the changes per 2 unit increase of n and apply that to the values of the functins when n =4. For f (n), the increase from n=2 to n=4 is 16.2−11.6=4.6. Thus, the value of f(6) is f(4)+4.6=16.2+4.6=20.8. The changwe in f (n) for n=2 to n=4 is 0.5−1.5=−1.So the value of g (6) is g(4)+(−1)=0.5−1=−0.5. Now, calculate h (6): h(6)=2×f(6)−g(6)=2(20.8)−(−0.5)=41.6+0.5=42.1. (D) is correct.
|
Topper's Solved these Questions
- FUNCTIONS BOOK - KAPLANCHAPTER - FUNCTIONS EXERCISE - FUNCTION NOTATION
1 Videos
- FUNCTIONS BOOK - KAPLANCHAPTER - FUNCTIONS EXERCISE - GRAPHS OF FUNCTIONS
1 Videos
- FUNCTIONS BOOK - KAPLANCHAPTER - FUNCTIONS EXERCISE - DESCRIBING REAL-LIFE SITUATIONS WITH FUNCTIONS
1 Videos
- EXPONENTS, RADICALS, POLYNOMIALS, AND RATIONAL EXPRESSIONSBOOK - KAPLANCHAPTER - EXPONENTS, RADICALS, POLYNOMIALS, AND RATIONAL EXPRESSIONSEXERCISE - RATIONAL EXPRESSIONS AND EQUATIONS
1 Videos
- GEOMETRY BOOK - KAPLANCHAPTER - GEOMETRY EXERCISE - THREE-DIMENSIONAL FIGURES
1 Videos
Similar Questions
Knowledge Check

The table above shows some values of the linear function f. Which of the following defines f ?Af(n)=n-3Bf(n) = 2n-4Cf(n) = 3n-5Df(n) = 4n-6
Some values of the linear function f are shown in the table above. What is the value of f (3) ?A6B7C8D9
Several values for the functions g (x) and h (x) are shown in the table above. What is the value of g(h(3)) ?A−1B0C3D6
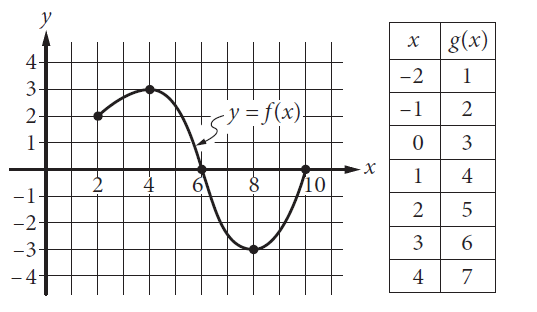
The complete graph of the function f and a table of values for the function g are shown above. The maximum value of f is k.What is the value of g(k) ?
View SolutionIf n(G−H)=15 and n(G∩H)=10, then find the value of n(G).
View SolutionIf f, g, h are real functions defined by f=√x+1, g(x)=1x and h(x)=2x2−3, then find the values of (2fg+g−h)(1) and (2f+g−h)(1).
View SolutionIf f, g, h are real functions defined by f=√x+1, g(x)=1x and h(x)=2x2−3, then find the values of (2fg+g−h)(1) and (2f+g−h)(1).
View SolutionLet f be a one-to-one function from set of natural numbers to itself such that f(mn)−f(m)×f(n) for all m,n∈N. what is least possible value of f(999)?
View Solution