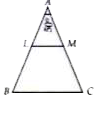
The tangent to the circumcircle of an isosceles ΔABC at A, in which AB= AC, is parallel to BC.
The correct Answer is:1
Step by step video, text & image solution for The tangent to the circumcircle of an isosceles DeltaABC at A, in which AB= AC, is parallel to BC. by Maths experts to help you in doubts & scoring excellent marks in Class 10 exams.
Updated on:21/07/2023Topper's Solved these Questions
- CIRCLESBOOK - EDUCART PUBLICATIONCHAPTER - CIRCLESEXERCISE - OBJECTIVE Type Questions (Very Short Questions)
10 Videos
- CIRCLESBOOK - EDUCART PUBLICATIONCHAPTER - CIRCLESEXERCISE - SHORT ANSWER (SA-I) Type Questions
28 Videos
- CIRCLESBOOK - EDUCART PUBLICATIONCHAPTER - CIRCLESEXERCISE - OBJECTIVE Type Questions (Fill in the Blanks)
9 Videos
- CBSE TERM-1 SAMPLE PAPER 2BOOK - EDUCART PUBLICATIONCHAPTER - CBSE TERM-1 SAMPLE PAPER 2EXERCISE - Section -C
7 Videos
- CONSTRUCTIONSBOOK - EDUCART PUBLICATIONCHAPTER - CONSTRUCTIONSEXERCISE - LONG ANSWER Type Questions
6 Videos
Similar Questions
Knowledge Check
In an isosceles ΔABC, if AC=BC and AB2=2AC2 then ∠C=?
A30∘B45∘C60∘D90∘DE is a tangent to the circumcircle of ΔABC at the vertex A such that DE∣∣BC. If AB=17cm, then the length of AC is equal to
A16.0cmB16.8cmC17.3cmD17cmO is the circumcentre of the isosceles ΔABC. Given that AB = AC = 17 cm and BC = 6 cm. The radius of the circle is
A3.015 cm.B3.205 cm.C3.025 cm.D3.125 cm.
In an isosceles ΔABC if ∠A=90∘ and AB=AC, find ∠B and ∠C.
View SolutionIn the adjoining figure, ΔABC is an isosceles triangle in which AB = AC. Side CP is parallel to AB and AP is the bisector of exterior angle CAD of Δ ABC. Prove that ∠PAC=∠BCAand□ABCP is a parallelogram.
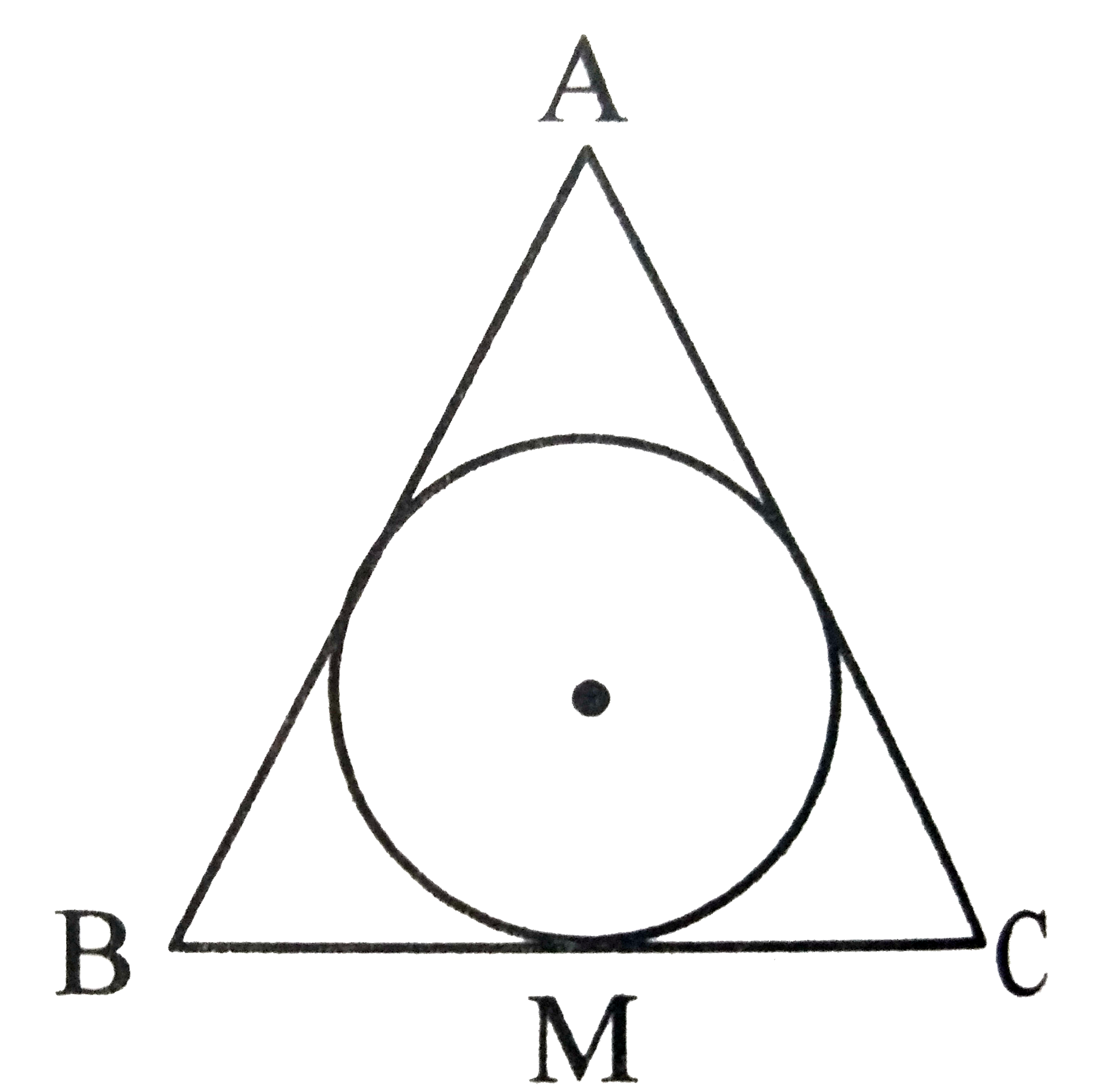
View SolutionIn the adjoining figure, the circle is the incircle of isosceles ΔABC, where seg AB=seg AC. Prove that M bisects BC.
View SolutionFind the area of an isosceles ΔABC in which BC = 8 cm and AB = AC = 5 cm. If CE⊥AB, find CE.
View SolutionAD is an altitude of an isosceles triangle ABC in which AB = AC. Show that
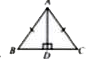
AD bisects BC
View Solution