Question

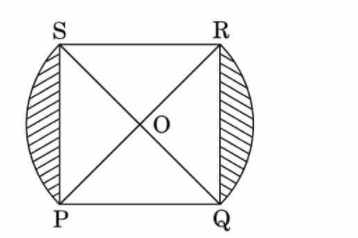
There are two circular flower beds on two sides of a square lawn ABCD of side 56 m. If the centre of each circular flower bed is the point of intersection of the diagonals of the square lawn, find the sum of the areas of the lawn and the flower beds.

Explanation

To solve the problem step by step, we will calculate the areas of the square lawn and the two circular flower beds, and then find their sum.

Step 1: Calculate the area of the square lawn

The area \( A \) of a square is given by the formula:
\( A = \text{side}^2 \)
Given that the side of the square lawn \( ABCD \) is 56 m, we can calculate the area as follows:
\( A = 56^2 = 3136 \text{ m}^2 \)

Step 2: Find the radius of the circular flower beds

The diagonals of the square intersect at the center point \( O \). The length of the diagonal \( d \) of a square can be calculated using the formula:
\( d = \text{side} \times \sqrt{2} \)
So, for our square:
\( d = 56 \times \sqrt{2} \)

The radius \( r \) of each circular flower bed can be found by noting that the radius is half the length of the diagonal:
\( r = \frac{d}{2} = \frac{56 \sqrt{2}}{2} = 28 \sqrt{2} \text{ m} \)

Step 3: Calculate the area of one circular flower bed

The area \( A_c \) of a circle is given by the formula:
\( A_c = \pi r^2 \)
Substituting the value of \( r \):
\( A_c = \pi (28 \sqrt{2})^2 = \pi \times 28^2 \times 2 = 2 \times 784 \pi = 1568 \pi \text{ m}^2 \)

Step 4: Calculate the area of two circular flower beds

Since there are two flower beds, the total area \( A_{total\_c} \) of the flower beds is:
\( A_{total\_c} = 2 \times A_c = 2 \times 1568 \pi = 3136 \pi \text{ m}^2 \)

Step 5: Calculate the total area

Now, we will find the total area \( A_{total} \) which is the sum of the area of the lawn and the area of the two flower beds:
\( A_{total} = A + A_{total\_c} = 3136 + 3136 \pi \)

Step 6: Approximate the total area using \( \pi \approx \frac{22}{7} \)

To get a numerical approximation, we can substitute \( \pi \) with \( \frac{22}{7} \):
\( A_{total} \approx 3136 + 3136 \times \frac{22}{7} \)
Calculating \( 3136 \times \frac{22}{7} \):
\( 3136 \times \frac{22}{7} = 3136 \times 3.142857 \approx 22000.5714 \)
Thus,
\( A_{total} \approx 3136 + 22000.5714 \approx 25136.5714 \text{ m}^2 \)

Final Answer

The sum of the areas of the lawn and the flower beds is approximately:
\( A_{total} \approx 25136.57 \text{ m}^2 \)

---