Through the point P(3,4) a pair of perpendicular lines are dranw which meet x-axis at the point A and B. The locus of incentre of triangle PAB is Solution in Tamil
x2−y2−6x−8y+25=0
x2+y2−6x−8y+25=0
x2−y2+6x+8y+25=0
x2+y2+6x+8y+25=0
The correct Answer is:1
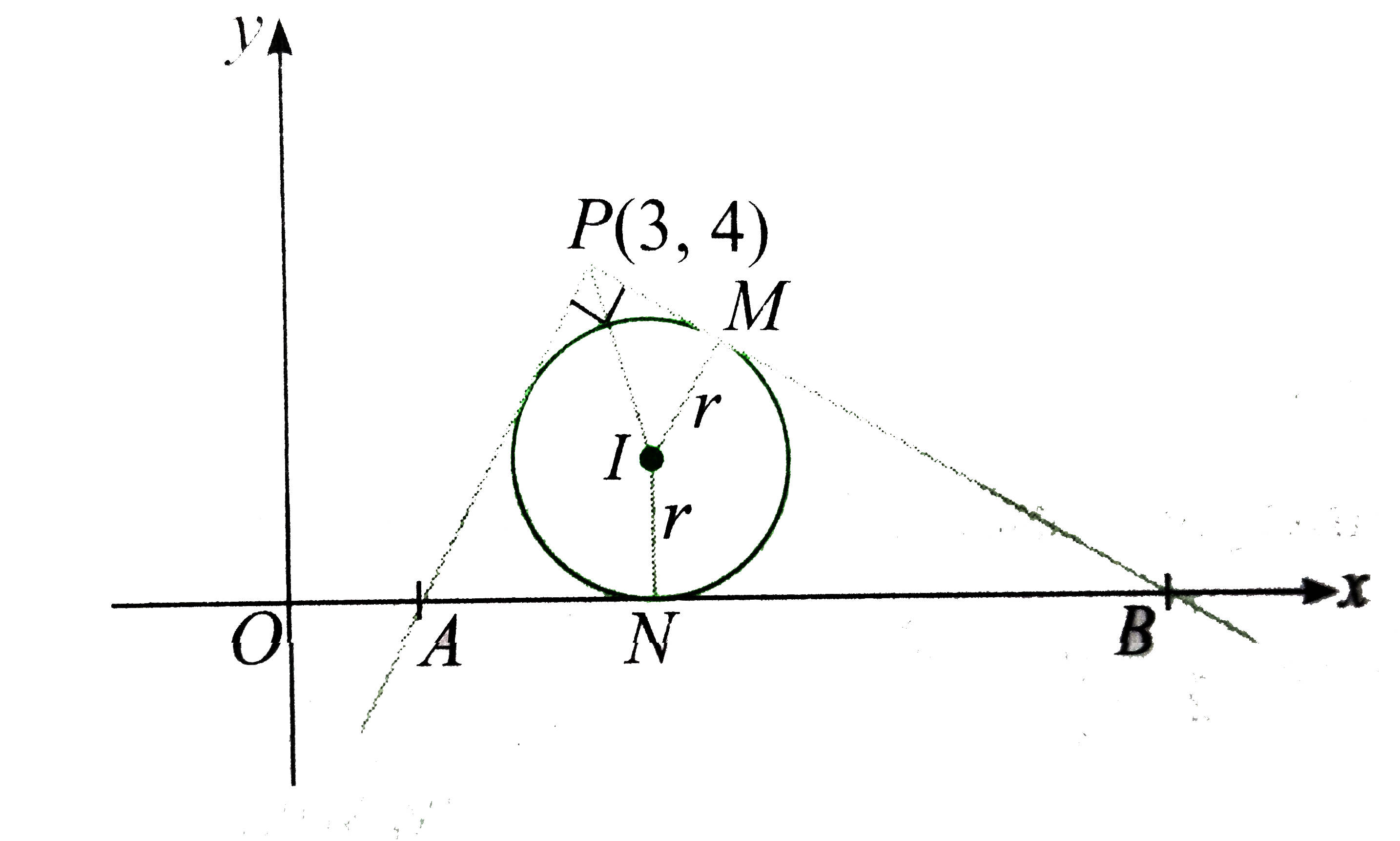
Let point I be (h,k).
From the figure,
IP=rcosec45∘, where r= inradius
⇒(IP)2=2r2
⇒(3−h)2+(4−k)2=2(|k|)2
( As circle touches x-axis, r=(|k|)2
⇒x2−y2−6x−8y+25=0, which is the require locus.
Topper's Solved these Questions
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise (Multiple)
25 Videos
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise (Comprehension)
46 Videos
- CIRCLE BOOK - CENGAGECHAPTER - CIRCLE EXERCISE - Exercise 4.6
5 Videos
- BINOMIAL THEOREMBOOK - CENGAGECHAPTER - BINOMIAL THEOREMEXERCISE - Comprehension
11 Videos
- CIRCLESBOOK - CENGAGECHAPTER - CIRCLESEXERCISE - Question Bank
16 Videos
Similar Questions
about to only mathematics
View SolutionEach side of a square is of length 6 units and the centre of the square Is ( - 1, 2). One of its diagonals is parallel to x+y=0. Find the co-ordinates of the vertices of the square.
View SolutionIf the circle x2+y2+2x+3y+1=0 cuts x2+y2+4x+3y+2=0 at AandB , then find the equation of the circle on AB as diameter.
View SolutionConsider a G.P. with first term (1+x)n, |x|<1, common ratio 1+x2 and number of terms (n+1). Let 'S' be sum of all the terms of the G.P., then
The coefficient of xn is 'S' is
View SolutionIf ax+by=10 is the chord of minimum length of the circle (x−10)2+(y−20)2=729 and the chord passes through (5,15) then the value of (4a+2b) is
View SolutionThe variable line drawn through the point (1,3) meets the x -axis at A and y -axis at B .If the rectangle OAPB is completed.Where O isthe origin,then locus of ^(-)P' is
View SolutionThe variable line drawn through the point (1,3) meets the x-axis at A and y -axis at B .If the rectangle OAPB is completed.Where O is the origin,then locus of P is
View SolutionThrough point P(−1,4), two perpendicular lines are drawn which intersect x-axis at Q and R. find the locus of incentre of ΔPQR.
View SolutionThrough the point P(3,4) a pair of perpendicular lines are dranw which meet x-axis at the point A and B. The locus of incentre of triangle PAB is
View SolutionA pair of perpendicular lines passing through P(1.4) intersect x-axis at Q and R, then the locus of incentre of ΔPQR is
View SolutionA straight line through the point (1,1) meets the X-axis at A and Y-axis at B. The locus of the mid-point of AB is
View SolutionA(2,3) and B(-3,4) be two given points. Find the equation of the locus of P so that the area of the triangle PAB is 8.5 sq.units.
View SolutionA (2,3),B(−3,4) are two points.If a point "P" moves such that the area of ΔPAB is 8.5 sq.Units then the locus of "P" is
View SolutionA(2,3) and B(-3,4) be two given points. Find the equation of the locus of P so that the area of the triangle PAB is 8.5 sq.units.
View SolutionThrough the point P(3,4) a pair of perpendicular lines are drawn which meet x-axis at the point A and B. The locus of incentre of triangle PAB is (a) x2−y2−6x−8y+25=0 (b) x2+y2−6x−8y+25=0 (c) x2−y2+6x+8y+25=0 (d) x2+y2+6x+8y+25=0
View Solutionबिंदु P से वृत x2+y2=4 पर स्पर्श रेखाऐं PA एवं PB
इस प्रकार खींची गई है की त्रिभुज PAB एक समबाहु त्रिभुज है
तो P का बिन्दुपथ होगा।
View Solution
