Tick the correct answer and justify: In ΔABC.AB = 6√3cm. AC = 12 cm and BC = 6 cm. The angle B is:
(A) 120 (B) 60 (C) 90 (D) 45
To find the angle B in triangle ABC where AB = 6√3 cm, AC = 12 cm, and BC = 6 cm, we can use the Pythagorean theorem. Here are the steps to solve the problem:
Step 1: Identify the sides of the triangle
We have the following sides:
- AB = 6√3 cm
- AC = 12 cm (this will be considered as the hypotenuse)
- BC = 6 cm
Step 2: Square the lengths of the sides
Now we will calculate the squares of the lengths of each side:
- AB2=(6√3)2=62⋅3=36⋅3=108 cm²
- AC2=122=144 cm²
- BC2=62=36 cm²
Step 3: Apply the Pythagorean theorem
According to the Pythagorean theorem, in a right triangle:
AC2=AB2+BC2
Substituting the values we calculated:
144=108+36
This simplifies to:
144=144
This confirms that triangle ABC satisfies the Pythagorean theorem.
Step 4: Determine the angle B
Since AC is the hypotenuse and the triangle satisfies the Pythagorean theorem, angle B, which is opposite to the hypotenuse AC, must be 90 degrees.
Conclusion
Thus, the correct answer is:
(C) 90 degrees
We have the following sides:
- AB = 6√3 cm
- AC = 12 cm (this will be considered as the hypotenuse)
- BC = 6 cm
Now we will calculate the squares of the lengths of each side:
- AB2=(6√3)2=62⋅3=36⋅3=108 cm²
- AC2=122=144 cm²
- BC2=62=36 cm²
According to the Pythagorean theorem, in a right triangle:
AC2=AB2+BC2
Substituting the values we calculated:
144=108+36
This simplifies to:
144=144
This confirms that triangle ABC satisfies the Pythagorean theorem.
Since AC is the hypotenuse and the triangle satisfies the Pythagorean theorem, angle B, which is opposite to the hypotenuse AC, must be 90 degrees.
Thus, the correct answer is:
(C) 90 degrees
Topper's Solved these Questions
Similar Questions
Knowledge Check
Tick the correct answer and justify : In ΔPQR, PQ = 6√3 cm , PR =12 cm and QR = 6 cm. The angle Q is :
A120∘B60∘C90∘D45∘In ΔABC, AB=6√3cm, AC=12cm and BC=6cm. Then ∠B is
A45∘B60∘C90∘D120∘In ΔABC,AB=6√3cm,AC=12cm,BC=6cm. Find measure of ∠A.
A30∘B60∘C90∘D45∘
In the figure, AC = 3 cm, BC = 6 cm and CD = 4 cm. Then sin A + cos B =

View SolutionIn ΔABC, angle B is right angle, AB = 12 cm and BC = 5 m. The value of sin C is :
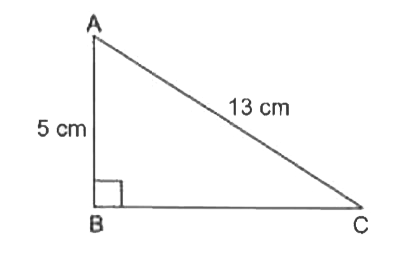
View SolutionIn △ABC, ∠B=90∘ , AB=5cm and AC=13cm. Then, BC = ?
View SolutionIf in ΔABC,∠B=90∘,AB=6√3 and AC=12cm, find BC.
View SolutionIn ΔABC,∠B is right angle, AB = 5 cm and BC = 12cm , then the value of cosC is :
View Solution
