To the circle x2+y2=4, two tangents are drawn from P(−4,0), which touch the circle at T1 and T2 . A rhomus PT1P'T2 s completed.
The circumcenter of triangle PT1T2 is at
2:1
1:2
√3:2
none of these
The correct Answer is:4
Clearly, PT1PT2 is rhombus
So, area of ΔPT1P' and that of ΔP'T1T2 are same.
Topper's Solved these Questions
- CIRCLE BOOK - CENGAGE ENGLISHCHAPTER - CIRCLE EXERCISE - NUMERICAL VALUE TYPE
21 Videos
- CIRCLE BOOK - CENGAGE ENGLISHCHAPTER - CIRCLE EXERCISE - ARCHIVES (JEE MAIN)
1 Videos
- CIRCLE BOOK - CENGAGE ENGLISHCHAPTER - CIRCLE EXERCISE - Linked Comprehension Type (For Problem 1-3)
3 Videos
- BINOMIAL THEOREMBOOK - CENGAGE ENGLISHCHAPTER - BINOMIAL THEOREMEXERCISE - Matrix
4 Videos
- CIRCLESBOOK - CENGAGE ENGLISHCHAPTER - CIRCLESEXERCISE - Comprehension Type
8 Videos
Similar Questions
To the circle x2+y2=4 two tangents are drawn from P(−4,0), which touch the circle at T1, and T2 and a rhombus PT1P'T2 is completed. Circumcentre of the triangle PT1T2 is at
View SolutionTo the circle x2+y2=4, two tangents are drawn from P(−4,0), which touch the circle at T1 and T2 . A rhomus PT1P'T2 s completed.
If P is taken to be at (h,0) such that P' lies on the circle, the area of the rhombus is
View SolutionTangents drawn from (2,0) to the circle x2+y2=1 touch the circle at AandB Then.
View SolutionThe tangent at any point on the ellipse 16x2+25y2=400 meets the tangents at the ends of the major axis at T1 and T2. The circle on T1T2 as diameter passes through
View SolutionTangents PT1,andPT2, are drawn from a point P to the circle x2+y2=a2. If the point P lies on the line Px+qy+r=0, then the locus of the centre of circumcircle of the triangle PT1T2 is
View SolutionTangents drawn from the point P(1,8) to the circle x2+y2−6x−4y−11=0 touch the circle at the points A&B ifR is the radius of circum circle of triangle PAB then [R]-
View SolutionA, B, C are respectively the points (1,2), (4, 2), (4, 5). If T1,T2 are the points of trisection of the line segment BC, the area of the Triangle AT1T2 is
View SolutionIf the tangents at t1 and t2 on y2=4ax meet on the directrix then
View SolutionIf the tangents at and t1 and t2= on y2=4ax meets on its axis then
View SolutionIf 'P' is in equilibrium then T1/T2 is
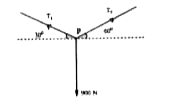
View Solution
