Two circle with radii r1 and r2 respectively touch each other externally. Let r3 be the radius of a circle that touches these two circle as well as a common tangents to two circles then which of the following relation is trueSolution in Tamil
1√a−1√b=1√c
c=2aba+b
1√a+1√b=1√c
c=2ab√a+√b
The correct Answer is:3
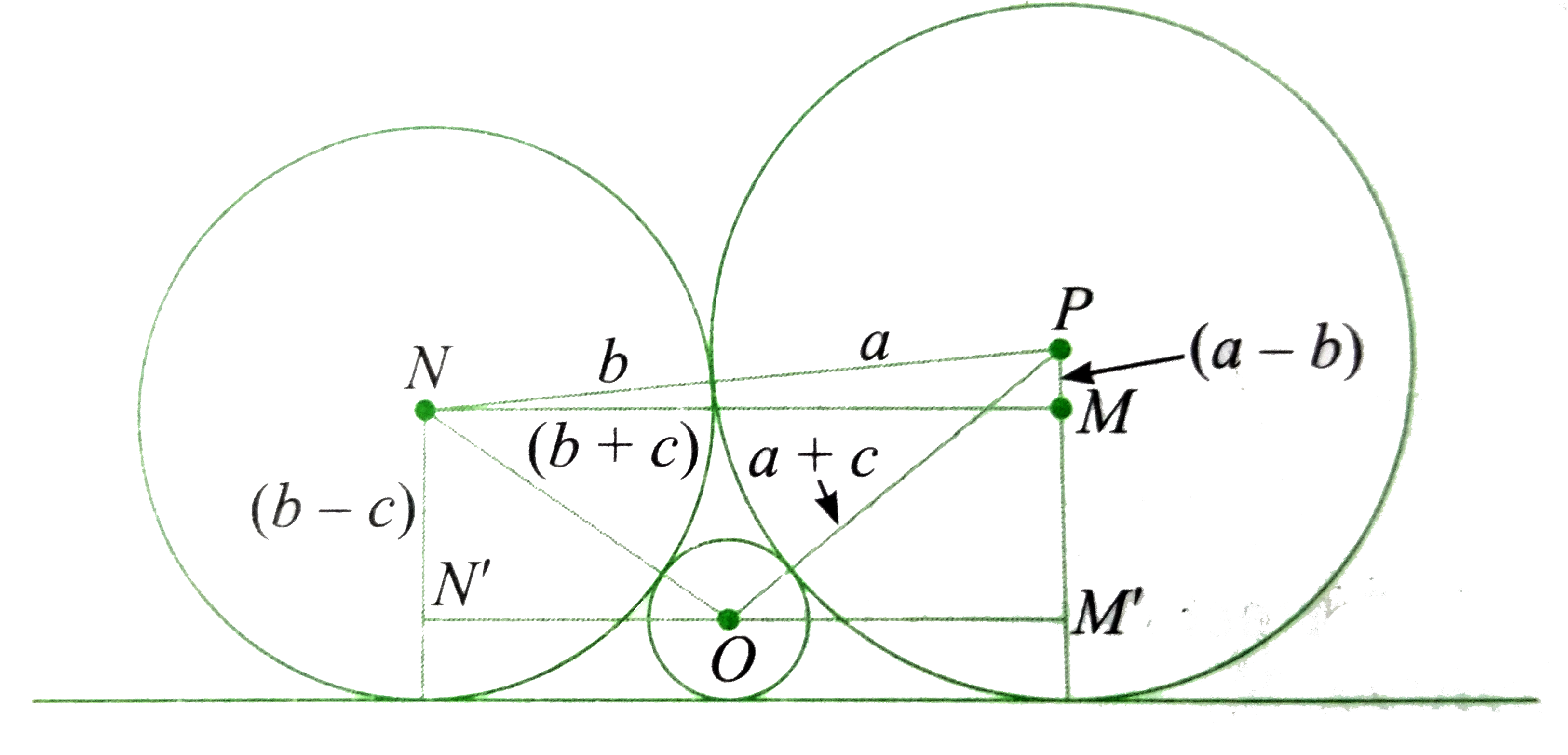
∵M'N'=MN
Now, MN=√(a+b)2+(a−b)2=√4ab
N'O=√(b+c)2−(b−c)2=√4bc
M'O=√(b+c)2−(a−c)2=√4ac
Now, N'O+M'O=MN
⇒2√ab=2√bc+2√ac
Dividing by 1√abc, we get
1√c=1√a+1√b
Topper's Solved these Questions
- CIRCLE Book:CENGAGEChapter:CIRCLE Exercise:Exercise (Multiple)
Explore 25 Videos
- CIRCLE Book:CENGAGEChapter:CIRCLE Exercise:Exercise (Comprehension)
Explore 46 Videos
- CIRCLE Book:CENGAGEChapter:CIRCLE Exercise:Exercise 4.6
Explore 5 Videos
- BINOMIAL THEOREMBook:CENGAGEChapter:BINOMIAL THEOREMExercise:Comprehension
Explore 11 Videos
- CIRCLESBook:CENGAGEChapter:CIRCLESExercise:Question Bank
Explore 16 Videos
Similar Questions
about to only mathematics
View SolutionEach side of a square is of length 6 units and the centre of the square Is ( - 1, 2). One of its diagonals is parallel to x+y=0. Find the co-ordinates of the vertices of the square.
View SolutionIf the circle x2+y2+2x+3y+1=0 cuts x2+y2+4x+3y+2=0 at AandB , then find the equation of the circle on AB as diameter.
View SolutionConsider a G.P. with first term (1+x)n, |x|<1, common ratio 1+x2 and number of terms (n+1). Let 'S' be sum of all the terms of the G.P., then
The coefficient of xn is 'S' is
View SolutionIf ax+by=10 is the chord of minimum length of the circle (x−10)2+(y−20)2=729 and the chord passes through (5,15) then the value of (4a+2b) is
View SolutionTwo fixed circles with radii r1andr2,(r1>r2) , respectively, touch each other externally. Then identify the locus of the point of intersection of their direction common tangents.
View SolutionTwo circles of radii r_(1) and r_(2)(r_(1)>r_(2)) touch each other exterally.Then the radius of circle which touches both of them externally and also their direct common tangent is (A) ( sqrtr_(1)+sqrt(r)_(2))^(2) (B) sqrt(r_(1)r_(2))(C)(r_(1)+r_(2))/(2) (D) (r_(1)-r_(2))/(2)
View SolutionTwo circles of radii r_(1) and r_(2), are both touching the coordinate axes and intersecting each other orthogonally.The value of (r_(1))/(r_(2)) (where r_(1)>r_(2)) equals -
View SolutionLet ABCD is a rectangle with AB=a & BC=b & circle is drawn passing through A & B and touching side CD. Another circle is drawn passing thorugh B & C and touching side AD. Let r1 & r2 be the radii of these two circle respectively.
r1r2 equals
View SolutionLet ABCD is a rectangle with AB=a & BC=b & circle is drawn passing through A & B and touching side CD. Another circle is drawn passing through B & C and touching side AD. Let r1 & r2 be the radii of these two circle respectively.
Minimum value of (r1+r2 equals
View SolutionThree circles C_(1),C_(2),C_(3) with radii r_(1),r_(2),r_(3)(r_(1)ltr_(2)ltr_(3)) respectively are given as r_(1)=2 , and r_(3)=8 they are placed such that C_(2) lines to the right of C_(1) and touches it externally C_(3) lies ot the right of C_(2) and touches it externally. There exist two stratight lines each of whic is a direct common tangent simultaneously to all the three circles then r_(2) is equal to
View SolutionTwo circle with radii r1 and r2 respectively touch each other externally. Let r3 be the radius of a circle that touches these two circle as well as a common tangents to two circles then which of the following relation is true
View SolutionThe locus of the centre of a variable circle touching two circles of radii r1, r2 externally , which also touch eath other externally, is conic. If r1r2=3+2√2, then eccentricity of the conic, is
View SolutionTwo circles of radii r1 and r2,r1>r2≥2 touch each other externally. If θ be the angle between the direct common tangents, then,
View SolutionTwo circles with radii a and b respectively touch each other externally . Let c be the radius of a circle that touches these two circles as well as a common tangent to the circles. Then
View Solution
