Two circles passing through A(1,2),B(2,1) touch the line 4x+8y−7=0 at C and D such that ACED in a parallelogram. Then:
The midpoint of AE must be the point of intersection of diagonals of parallelogram.
Let E≡(h,k).
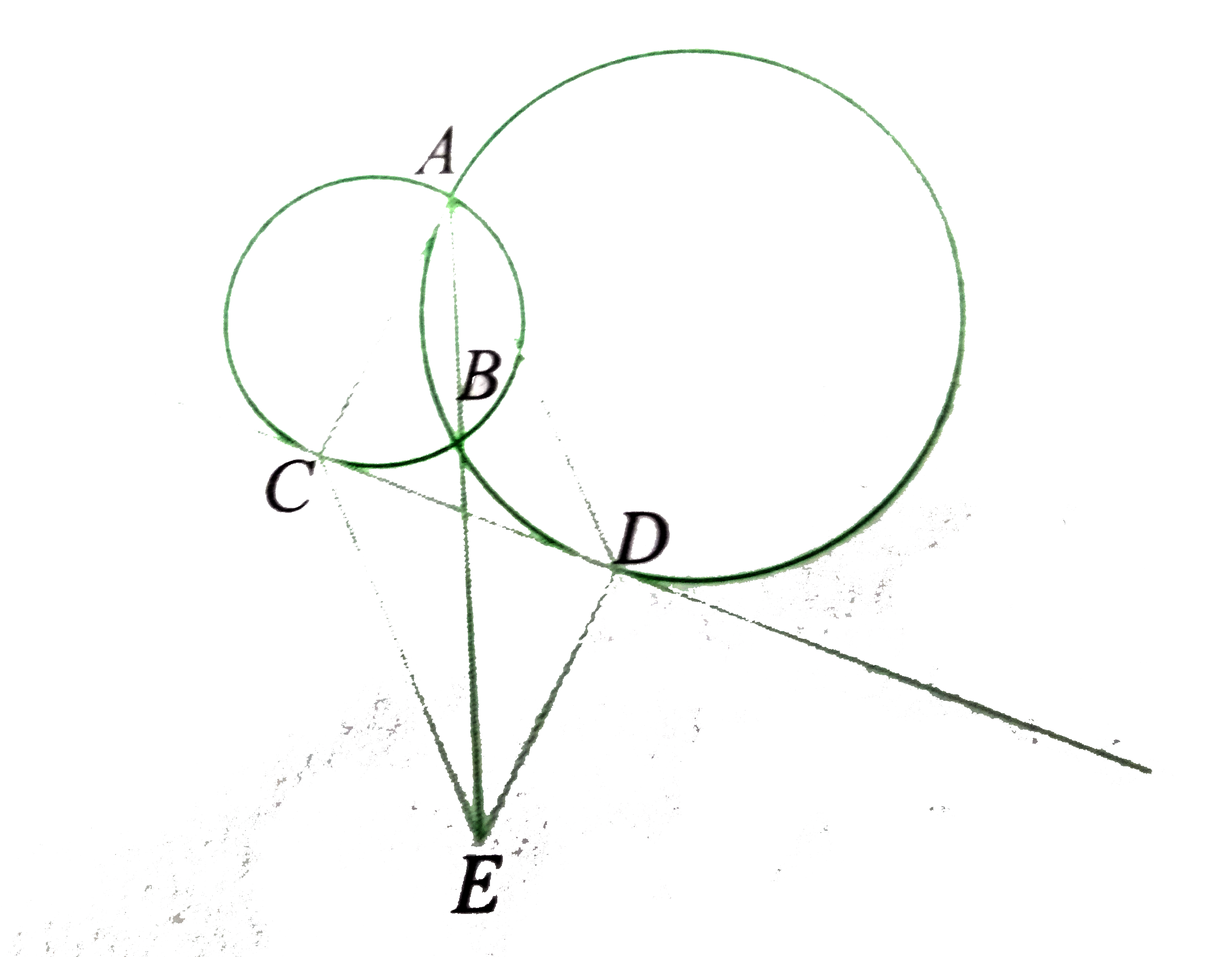
So, (h+12,k+22) must lie on common tangent 4x+8y−7=0.
∴2h+4k+3=0 (1)
Also, (h,k) lies on AB whose equation is x+y=3.
∴h+k=3 (2)
Solving (1) and (2) , we get
h=152,k=−92
Topper's Solved these Questions
- CIRCLE Book:CENGAGEChapter:CIRCLE Exercise:Exercise 4.1
Explore 14 Videos
- CIRCLE Book:CENGAGEChapter:CIRCLE Exercise:Exercise 4.2
Explore 5 Videos
- BINOMIAL THEORMBook:CENGAGEChapter:BINOMIAL THEORMExercise:Question Bank
Explore 31 Videos
- CIRCLESBook:CENGAGEChapter:CIRCLESExercise:Question Bank
Explore 32 Videos
Similar Questions
Two circles C1andC2 both pass through the points A(1,2)andE(2,1) and touch the line 4x−2y=9 at BandD, respectively. The possible coordinates of a point C, such that the quadrilateral ABCD is a parallelogram, are (a,b). Then the value of |ab| is_________
View SolutionCentre of the circles passing through the point (−4,3) and touching the lines x+y=2 and x−y=2 is
View Solution
Knowledge Check
Equation of circle passing through A(-1,-3), B (3,0)
and touching line 4x+3y−12=0 at B , isAx2+y2−2x−3y−3=0Bx2+y2−2x−3y−3=0Cx2+y2−2x−3y+3=0Dx2+y2−2x+3y−3=0A circle passes through the point (-1,7) and touches the line y = x at (1, 1). Its diameter is
A4√2B5C5√2D6Equation of circle which passes through (-1,2) and
(1,2) , and touches the line y = 5 , isA9x2+9y2−60y+75=0B9x2+9y2−60−75=0C9x2+9y2+60y−75=0D9x2+9y2+60+75=0
A circle passes through a point (2,8) and touches the lines 4x−3y−24=0and4x+3y+42=0 and centre lies on the line x=λ then (−4λ) is
View SolutionCentre of a circle passing through point (0,1) and touching the curve y=x2 at (2,4) is
View SolutionThe equation of the line passing through (1,-2) and parallel to the line 8x-4y+7=0 is
View SolutionCentre of a circle passing through point (0,1) and touching the curve y=x2 at (2,4) is
View SolutionCentre of a circle passing through point (0,1) and touching the curve y=x2 at (2,4) is
View Solution
