Two circles touch each other externally at . is a common tangent to the circle touching them at and . The value of is (a) (b) (c) (d)
To solve the problem, we need to find the value of angle ∠APB where two circles touch each other externally at point P and AB is a common tangent to the circles touching them at points A and B.
1. Identify the Angles:
- Let ∠CAP=α and ∠CBP=β.
- Since CA and CP are tangents from point C to the circle, we know that CA=CP. Therefore, ∠APC=α (by the property of isosceles triangles).
- Similarly, since CB and CP are tangents from point C to the circle, we have CB=CP. Thus, ∠CPB=β.
2. Express ∠APB:
- The angle ∠APB can be expressed as:
∠APB=∠APC+∠BPC=α+β
3. Consider Triangle PAB:
- In triangle PAB, the sum of the angles is equal to 180∘:
∠PAB+∠PBA+∠APB=180∘
- Here, ∠PAB=α+β and ∠PBA=β+α (since both angles are equal by the property of isosceles triangles).
4. Set Up the Equation:
- Substituting the known angles into the equation gives:
(α+β)+(α+β)+∠APB=180∘
- This simplifies to:
2(α+β)+∠APB=180∘
5. Substituting ∠APB:
- Since ∠APB=α+β, we can replace it in the equation:
2(α+β)+(α+β)=180∘
- This simplifies to:
3(α+β)=180∘
6. Solve for α+β:
- Dividing both sides by 3 gives:
α+β=60∘
7. Final Calculation:
- Since ∠APB=α+β, we find:
∠APB=60∘
Conclusion:
The value of ∠APB is 60∘. Therefore, the correct answer is option (c) 60∘.
- Let ∠CAP=α and ∠CBP=β.
- Since CA and CP are tangents from point C to the circle, we know that CA=CP. Therefore, ∠APC=α (by the property of isosceles triangles).
- Similarly, since CB and CP are tangents from point C to the circle, we have CB=CP. Thus, ∠CPB=β.
- The angle ∠APB can be expressed as:
∠APB=∠APC+∠BPC=α+β
- In triangle PAB, the sum of the angles is equal to 180∘:
∠PAB+∠PBA+∠APB=180∘
- Here, ∠PAB=α+β and ∠PBA=β+α (since both angles are equal by the property of isosceles triangles).
- Substituting the known angles into the equation gives:
(α+β)+(α+β)+∠APB=180∘
- This simplifies to:
2(α+β)+∠APB=180∘
- Since ∠APB=α+β, we can replace it in the equation:
2(α+β)+(α+β)=180∘
- This simplifies to:
3(α+β)=180∘
- Dividing both sides by 3 gives:
α+β=60∘
- Since ∠APB=α+β, we find:
∠APB=60∘
The value of ∠APB is 60∘. Therefore, the correct answer is option (c) 60∘.
Topper's Solved these Questions
Similar Questions
Two equal circles touch each other externally at C and AB is a common tangent to the circles. Then, ∠ACB= 60o (b) 45o (c) 30o (d) 90o
View SolutionTwo circles touch each other externally at point P. Q is a point on the common tangent through P. Prove that the tangents QA and QB are equal.
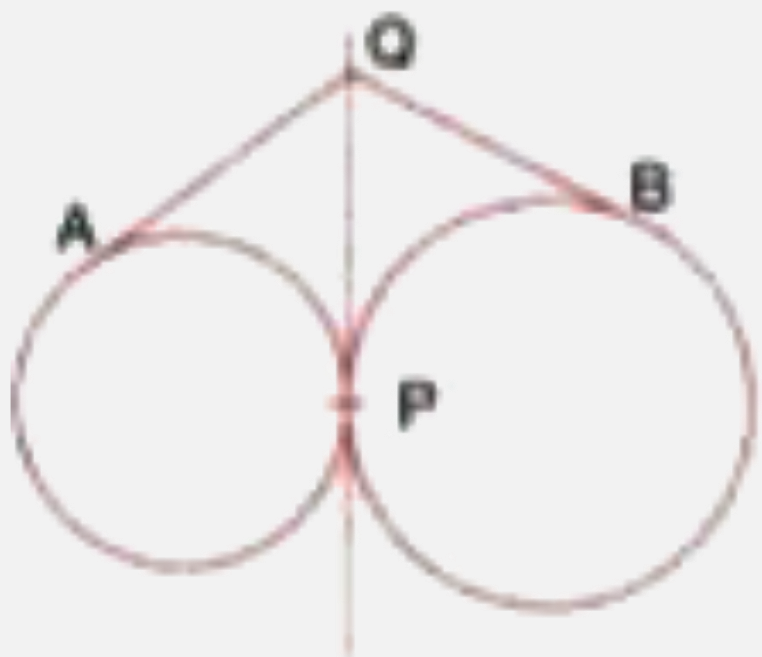 View Solution
View Solution
Knowledge Check
- Question 1 - Select One
A and B are centers of two circles that touch each other externally, as shown in the figure.What is the area of the circle whose diameter is AB?
 A4πB25π/4C9πD16π
A4πB25π/4C9πD16π
3 circles of radii a,b,c(a<b<c) touch each other externally and have x-axis as a common tangent then
View SolutionIn Figure, two circles touch each other at the point C . Prove that the common tangent to the circles at C , bisects the common tangent at P and Q .
View SolutionIn the given figure, two circles touch each other externally at point P. AB is the direct common tangent of these circles. Prove that:
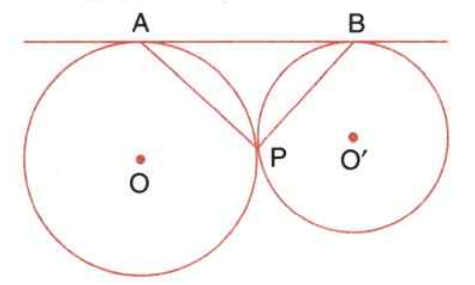
(i) tangent at point P bisects AB
(ii) angle APB=90∘View SolutionIn the figure, two circles touch each other at the point C.Prove that the common tangents to the circles at C, bisect the common tangents at P and Q.
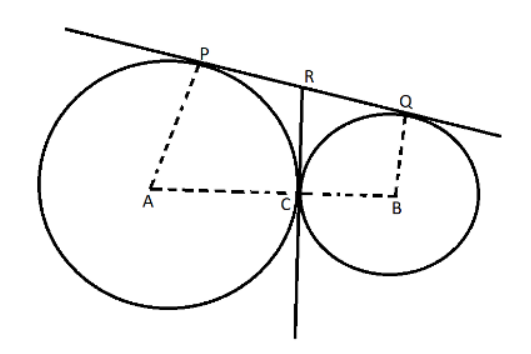 View Solution
View SolutionIn Figure, PA and PB are tangents to the circle with centre O such that ∠APB=50∘ . Write the measure of ∠OAB .
View SolutionIf PT is tangent drawn from a point P to a circle touching it at T and O is the centre of the circle, then ∠OPT+∠POT= (a)30∘ (b)60∘ (c)90∘ (d)180∘
View SolutionIn Figure, APB is a tangent to a circle with centre O at point P . If ∠QPB=50∘ , then the measure of ∠POQ is (a)100∘ (b) 120∘ (c) 140∘ (d) 150∘
View Solution

